Числа в форме с плавающей запятой

От недостатков ФЗ в значительной степени свободна форма представления чисел с плавающей запятой (ПЗ), известная также под названиями нормальной или полулогарифмической формы. В данном варианте каждое число разбивается на две группы цифр. Первая группа цифр называется мантиссой, вторая — порядком. Число представляется в виде произведения

X = ± mq^±p,

где т – мантисса числа X, р – порядок числа, q – основание системы счисления.

Для представления числа в форме с ПЗ требуется задать знаки мантиссы и порядка, их модули в q-ичном коде, а также основание системы счисления q. Формат представления числа с ПЗ показан на рисунке 2.16. Нормальная форма неоднозначна, так как взаимное изменение m и p приводит к «плаванию» запятой, чем и обусловлено название этой формы.

Диапазон и точность представления чисел с ПТ зависят от числа разрядов, отводимых под порядок и мантиссу. На рисунке 2.17 показаны диапазоны разрядностей порядка и мантиссы, характерные для известных ЭВМ.

В большинстве вычислительных машин для упрощения операций над порядками последние приводят к целым положительным числам, применяя так называемый смещенный порядок. Для этого к истинному порядку добавляется целое положительное число – смещение. Например, в системе со смещением 128 порядок «–3» представляется как «125» (–3 + 128). Обычно смещение выбирается равным половине представимого диапазона порядков. Отметим, что смещенный порядок занимает все биты поля порядка, в том числе и тот, который ранее использовался для записи знака порядка.

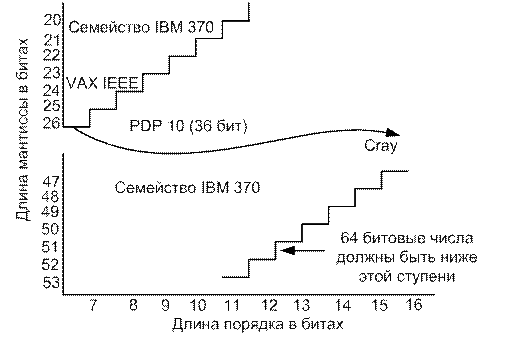
Рисунок 2.17 – Типовые разрядности порядка и мантиссы

Мантисса в числах с ПЗ обычно представляется в нормализованной форме. Это означает, что на мантиссу налагаются такие условия, чтобы она по модулю была меньше единицы, а первая цифра после точки отличалась от нуля. Полученная таким образом мантисса называется нормализованной.

Для представления числа с ПЗ в ЭВМ используется база 2 (q = 2). При этом применяют еще один способ повышения точности представления мантиссы, называемый приемом скрытой единицы. Суть его в том, что в нормализованной мантиссе старшая цифра всегда равна единице, следовательно, эта цифра может не записываться, а подразумеваться. Запись мантиссы начинают с ее второй цифры, и это позволяет задействовать дополнительный значащий бит для более точного представления числа. Следует отметить, что значение порядка в данном случае не меняется. Скрытая единица перед выполнением арифметических операций восстанавливается, а при записи результата — удаляется. Таким образом, нормализованная мантисса 0,101000(1) при использовании способа «скрытой единицы» будет иметь вид 0,010001 (в скобках указана цифра, не поместившаяся в поле мантиссы при стандартной записи).

Для более существенного увеличения точности вычислений под число отводят несколько машинных слов, например два. Дополнительные биты, как правило, служат для увеличения разрядности мантиссы, однако в ряде случаев часть из них может отводиться и для расширения поля порядка. В процессе вычислений может получаться ненормализованное число. В таком случае ЭВМ, если это предписано командой, автоматически нормализует его.

Примеры. На рисунке 2.18 представлен типичный 32-битовый формат числа с ПЗ. Старший (левый) бит содержит знак числа. Значение смешенного порядка хранится в разрядах с 1-го по 8-й и может находиться в диапазоне от 0 до 255. Для получения фактического значения порядка из содержимого этого поля нужно вычесть фиксированное значение, равное 128. С таким смещением фактические значения порядка могут лежать в диапазоне от -128 до +127. Третье поле слова содержит нормализованную мантиссу со скрытым разрядом (единицей). Благодаря такому приему 23-разрядное поле позволяет хранить 24-разрядную мантиссу в диапазоне от 0,5 до 1,0.

Рисунок 2.18 – 32-битовый формат числа с ПЗ

На рис. 2.19 приведены диапазоны чисел, которые могут быть записаны с помощью 32-разрядного слова.

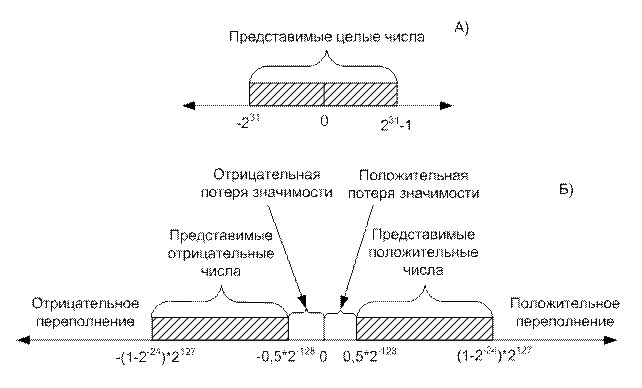
Рисунок 2.19 – Числа, представимые в 32-битовых форматах:

А) – целые числа; Б) – числа с ПЗ

В варианте для целых чисел в дополнительном коде могут быть представлены все целые числа от -2³¹ до (2³¹ – 1), то есть всего 2³² различных чисел (см. рисунок 2.19, А).

Для случая ПЗ представимы два диапазона чисел (см. рисунок 2.19, Б):

отрицательные числа: –(1-2^–24)*2¹²⁷ ≤ X ≤ –0,5*2^–128;

положительные числа: 0,5*2^–128 ≤ X ≤ (1-2^–24)*2¹²⁷.

В эту область не включены пять участков:

отрицательные числа, меньшие чем –(1-2^–24)*2¹²⁷ – отрицательное переполнение;

отрицательные числа, большие чем –0,5*2^–128 – отрицательная потеря значимости;

положительные числа, меньшие чем 0,5*2^–128 – положительная потеря значимости;

положительные числа, большие чем (1-2^–24)*2¹²⁷ – положительное переполнение.

Показанная запись числа с ПЗ не учитывает нулевого значения. Для этой цели используется специальная кодовая комбинация. Переполнения возникают, когда в результате арифметической операции получается значение большее, чем можно представить порядком 127. При переполнении, как правило, выдается соответствующее сообщение и выполнение программы прекращается. Потеря значимости – это когда результат представляет собой слишком маленькое дробное значение. Потеря значимости является менее серьезной проблемой, поскольку такой результат обычно рассматривают как нулевой.

Кроме этого, числа в форме с ПЗ, в отличие от чисел в форме с ФЗ, размешены на числовой оси неравномерно. Расстояние между соседними представимыми числами увеличивается с ростом порядка n. Возможные значения в начале числовой оси расположены плотнее, а по мере движения вправо – все реже, что иллюстрирует рисунок 2.20. Это означает, что чаще всего вычисления приводят к результату, который не является точным, а представляет собой округление до ближайшего представимого значения.

Рисунок 2.20 – Плотность представимых чисел с ПЗ на числовой оси

Для формата с ПЗ имеет место противоречие между диапазоном и точностью. Если увеличить число битов, отведенных под порядок, расширяется диапазон представимых чисел. Однако, поскольку может быть представлено только фиксированное число различных значений, уменьшается плотность и тем самым точность. Единственный путь увеличения как диапазона, так и точности – увеличение количества разрядов, поэтому в большинстве ЭВМ предлагается использовать числа в одинарном и двойном форматах. Например, число одинарного формата может занимать 32 бита, а двойного (double) – 64 бита.

Числа с плавающей запятой в разных ЭВМ имеют несколько различных форматов. В настоящее время для всех ЭВМ рекомендован стандарт, разработанный общепризнанным международным центром стандартизации IEEE (Institute of Electrical and Electronics Engineers). Этот стандарт был разработан с целью облегчить перенос программ с одного процессора на другие и нашел широкое применение практически во всех процессорах и арифметических сопроцессорах.

Стандарт определяет 32-битовый (float) и 64-битовый (double) форматы с 8- и 11-разрядным порядком, соответственно. Основанием системы счисления является 2.

Не все кодовые комбинации в форматах ШЕЕ интерпретируются обычным путем – некоторые комбинации используются для представления специальных значений. Предельные значения порядка, содержащие все нули (0) и все единицы (255 — в одинарном формате и 2047 — в двойном формате), определяют специальные значения. Нулевой порядок совместно с нулевой мантиссой представляют положительный или отрицательный 0, в зависимости от состояния бита знака мантиссы. Порядок, содержащий единицы во всех разрядах, совокупно с нулевой мантиссой представляют положительную или отрицательную бесконечность, в зависимости от состояния бита знака, что позволяет пользователю самому решить, считать ли это ошибкой или продолжать вычисления со значением, равным бесконечности. Кодовая комбинация, в которой порядок содержит все единицы, а мантисса не равна 0, используется как признак «не числа» (NAN — Not a Number) и служит для предупреждения о различных исключительных ситуациях.

Дата добавления: 2013-12-12