МОДУЛЬ 1: векторы, прямые и плоскости

ЛЕКЦИИ

АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ

для ИБМ, МТ, РК, СМ-7, СМ-11, СМ-13, Э-5. 1 курс, 1-й семестр, 2012-13

Лекция 1. Скалярные и векторные величины. Понятие геометрического вектора как направленного отрезка. Нуль-вектор, единичный вектор (орт). Коллинеарные и компланарные векторы. Равенство векторов. Связанные, скользящие, свободные векторы. Линейные операции над векторами, свойства этих операций. Ортогональная проекция векторов на направление. Теоремы о проекциях. Линейная комбинация векторов. Линейная зависимость векторов. Критерий линейной зависимости двух и трех векторов. Линейная зависимость четырех векторов.

Лекция 2. Базис. Разложение вектора по базису. Координаты вектора. Линейные операции над векторами, заданными своими координатами. Ортонормированный базис i, j, k. Скалярное произведение векторов, его механический смысл. Формула для скалярного произведения векторов, заданных своими координатами в базисе i, j, k. Вычисление длины вектора, косинуса угла между векторами и проекции вектора на направление. Равенство координат вектора в ортонормированном базисе проекциям этого вектора на направления соответствующих базисных векторов. Направляющие углы вектора, свойство их косинусов.

Лекция 3. Ориентация базиса, правые и левые тройки векторов. Векторное произведение двух векторов, его механический и геометрический смысл. Свойства векторного произведения (дистрибутивность без док-ва). Вычисление векторного произведения в координатной форме в ортонормированном базисе. Смешанное произведение трех векторов и его геометрический смысл. Объем тетраэдра. Свойства смешанного произведения. Вычисление смешанного произведения в ортонормированном базисе. Условие компланарности трех векторов. Проверка ориентации тройки векторов.

Лекция 4. Декартова прямоугольная система координат на плоскости и в пространстве. Радиус-вектор точки, координаты точки; связь координат вектора с координатами его начала и конца. Геометрический смысл уравнения 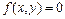на плоскости и в пространстве и уравнения 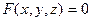. Поверхность, заданная уравнением 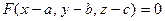. Формулы для расстояния между двумя точками и деления отрезка в данном отношении. Прямая на плоскости, её направляющий и нормальный векторы. Различные виды уравнения прямой на плоскости: с угловым коэффициентом, параметрические уравнения, каноническое уравнение, уравнение в отрезках, общее уравнение. Взаимное расположение двух прямых на плоскости. Нахождение угла между прямыми. Расстояние от точки до прямой на плоскости.

Лекция 5. Уравнение плоскости, проходящей через заданную точку перпендикулярно заданному вектору. Общее уравнение плоскости. Уравнение плоскости, проходящей через три точки, не лежащие на одной прямой. Уравнение плоскости “в отрезках”. Взаимное расположение двух плоскостей, угол между плоскостями. Расстояние от точки до плоскости. Расположение заданной точки относительно сторон плоскости. Прямая в пространстве. Общие уравнения прямой. Параметрические уравнения прямой (в векторной и координатной форме), канонические уравнения прямой в пространстве. Уравнения прямой, проходящей через две заданные точки. Пучок плоскостей.

Лекция 6. Вычисление расстояния от точки до прямой в пространстве. Взаимное расположение прямой и плоскости. Нахождение точки пересечения прямой и плоскости. Взаимное расположение двух прямых в пространстве. Нахождение точки пересечения двух пересекающихся прямых и расстояния между двумя параллельными или скрещивающимися прямыми. Угол между двумя прямыми, между прямой и плоскостью.

Дата добавления: 2013-12-12