Закономерности движения подземных вод

Основной закономерностью является приведенный ранее закон Дарси, который можно записать также в объемной форме:

Q = k A I. (1)

С использованием зависимости (1) решаются разнообразные задачи – определение расхода потока, дебита скважин, притока воды в котлованы и к водозаборам и др.

Например, определим расход потока Q, т.е. объем воды, переносимый им в единицу времени. Пусть вода фильтрует на расстояние L в слое шириной В (см. рис. 4.1). Подставляя в формулу для Q выражения A = (H + h)B/2 и I = (H – -h)/L, получаем нужную формулу:

Q = k (H² – h²)B/2L. (2)

При решении практических задач используют удельный расход – расход в единицу времени на единицу ширины потока, то есть Q₁ = k (H² – h²)/2L.

Рассмотрим определение притока к водозаборам. Они могут быть горизонтальными (канава, водосборная галерея) и вертикальными (скважина, колодец). Если водозабор вскрывает водоносный слой на всю его мощность, он называется совершенным; в противном случае – несовершенным.

Откачка воды сопровождается понижением уровня воды в скважине, распространяющимся на некоторое расстояние – радиус влияния R. Вокруг скважины образуется депрессионная воронка. Примерные значения радиуса влияния: для гравия 1км, крупного песка 0,5 км, мелкого 100…200м, для суглинка 50 м.

Определим приток к совершенному горизонтальному водозабору – канаве, пройденной вдоль потока, с шириной 2а и длиной L (рис. 5.3).

Рассматриваем установившийся режим, когда с каждой стороны поток фильтрует через поперечное сечение A = y L при градиенте напора I = dy/dx. Подставляя эти выражения в формулу (1), разделяя переменные, интегрируя и разрешая относительно q, получаем:

Q = k L (H² – h²)/ (R – a).

Поскольку a<<R, поправка на полуширину практического значения не имеет и можно принять

Q = k L (H² – h²)/ R и соответственно Q₁ = k (H² – h²)/R.

В таком виде формула непосредственно следует из (2) при замене B на L и удвоении притока.

Точно также получается решение для вертикального водозабора – скважины диаметром 2а. Согласно схеме на рис.5.3, в этом случае площадь будет A = 2π xy. Проводя далее решение аналогично предыдущему, получаем формулу Дюпюи:

Q = πk(H² – h²)/(lnR – lna).

Для напорных подземных вод порядок вывода формул расхода аналогичен.

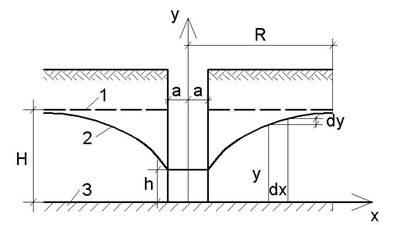
Рис. 5.3. Схема к определению притока к горизонтальному водозабору:

1 – УГВ; 2 – кривая депрессии; 3 - водоупор

Дата добавления: 2013-12-12