Плоскостей проекций

Положение плоскости относительно

Любая произвольно взятая в пространстве плоскость может занимать общее или частное положение.

Плоскостью общего положения называется плоскость, которая не перпендикулярна и не параллельна ни к одной из плоскостей проекций (см. рис. 5.2). Все остальные плоскости относятся к плоскостям частного положения и подразделяются на проецирующие плоскости и плоскости уровня.

Проецирующей называется плоскость, перпендикулярная к одной из плоскостей проекций. Например, горизонтально-проецирующая плоскость перпендикулярна к горизонтальной плоскости проекции П₁ (рис. 5.3).

Рис. 5.3

Горизонтальные проекции всех геометрических объектов (точек, прямых, фигур), лежащих в этой плоскости, совпадают с горизонтальным следом 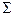₁. Угол β, который образуется между плоскостями Σ и П₂, проецируется на П₁ без искажения. Фронтальный след 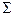₂ перпендикулярен к оси x. Фронтально-проецирующая плоскость 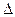() перпендикулярна к фронтальной плоскости П₂ (рис. 5.4).

Фронтальные проекции всех геометрических объектов (точек, прямых, фигур), лежащих в этой плоскости, совпадают с фронтальным следом плоскости 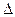₂. Угол α, который образуется между заданной плоскостью 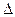и П₁, проецируется на П₂ без искажения. Горизонтальный след плоскости 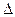₁ перпендикулярен к оси x.

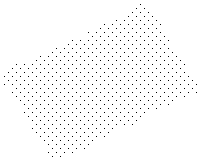Рис. 5.4

Профильно - проецирующая плоскость Т (T₁, T₂) перпендикулярна к профильной плоскости проекции П₃ (рис. 5.5).

а) б)

Рис. 5.5

Профильные проекции всех геометрических объектов, лежащих в этой плоскости, совпадают с профильным следом плоскости Т₃.

Углы α и β, которые образуются между заданной плоскостью и плоскостями проекций П₁ и П₂ (угол α = углу наклона плоскости T к плоскости проекции П₁; угол β = углу наклона плоскости Т к плоскости проекций П₂), плоскость Т проецируются на плоскость П₃ без искажений. Горизонтальный и фронтальный следы плоскости параллельны оси х.

Профильно-проецирующая плоскость может проходить через ось x (рис. 5.6).

Следы такой плоскости 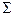₁ ≡ 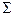₂ совпадают друг с другом и с осью x, поэтому не определяют положение плоскости в системе двух плоскостей проекций. Необходимо кроме следов задать в плоскости точку (рис. 5.6). В частном случае эта плоскость может быть биссекторной плоскостью, если угол α = β, а точка А равноудалена от плоскостей проекций П₁ и П₂.

Рис. 5.6

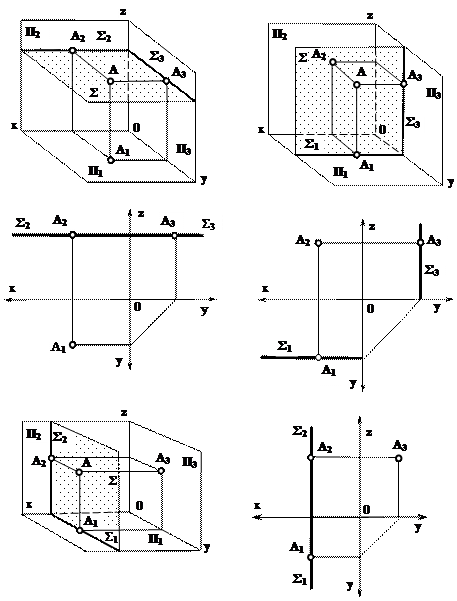
Плоскостью уровня называется плоскость, перпендикулярная одновременно к двум плоскостям проекций и параллельная третьей. Таких плоскостей может быть три разновидности (рис. 5.7):

· горизонтальная плоскость параллельна плоскости П₁ и перпендикулярна к П₂, П₃ (рис. 5.7, а);

· фронтальная плоскость параллельна плоскости П₂ и перпендикулярна к П_1, П₃ (рис. 5.7, б);

· профильная плоскость параллельна плоскости П₃ и перпендикулярна к П_1, П₂ (рис. 5.7 в).

а) б)

в)

Рис. 5.7

Из определения плоскостей уровня следует, что одна из проекций точки, линии, фигуры, принадлежащих этим плоскостям, будет совпадать с одноименным следом плоскости уровня, а другая проекция будет натуральной величиной этих геометрических образов

Дата добавления: 2013-12-12