
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Основные положения
|
|
|
|
К ПЛОСКОСТИ
ПРЯМАЯ ЛИНИЯ, ПЕРПЕНДИКУЛЯРНАЯ
Параллельность прямой и плоскости
Прямая и плоскость параллельны, если в плоскости имеется прямая, параллельная заданной прямой.
7.3.1 Задание: построить проекции прямой, проходящей через точку А и параллельной прямой m,принадлежащей плоскости Σ (BCD) (рис. 7.5).
 |
Рис. 7.5
Решение: в условии задачи задана фронтальная проекция m2 прямой m. Находим горизонтальную проекцию m1 прямой m. Условия параллельности прямой и плоскости: прямая параллельна плоскости, если она параллельна какой-то прямой, расположенной в данной плоскости.
Используя это условие, строят проекции искомой прямой, проходящие через точку А; n1 проводятся параллельно m1, n2 — параллельно m2.
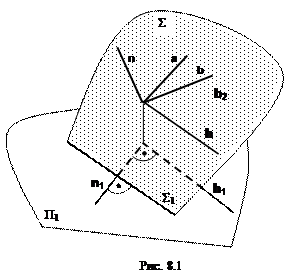
Обратимся к рисунку 8.1, на котором изображена плоскость 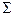 и перпендикулярная к ней прямая n.
и перпендикулярная к ней прямая n.
Прямая n перпендикулярна к любой прямой плоскости 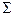 , т.е.
, т.е.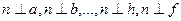 . Каждый такой прямой угол проецируется на плоскость проекций в виде некоторого угла, но угол между прямой n и горизонталью плоскости h проецируется на горизонтальную плоскость проекций в виде прямого угла, так как его сторона параллельна плоскости П1 (h || П1).
. Каждый такой прямой угол проецируется на плоскость проекций в виде некоторого угла, но угол между прямой n и горизонталью плоскости h проецируется на горизонтальную плоскость проекций в виде прямого угла, так как его сторона параллельна плоскости П1 (h || П1).
Если 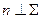 , то
, то 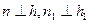 .
.
 |
Угол между прямой n фронталью f плоскости проецируется на фронтальную плоскость проекций прямым углом (его сторона 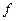 || П2).
|| П2).
Если 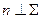 , то
, то 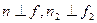 .
.
Если прямая перпендикулярна к плоскости, то ее проекции перпендикулярны к одноименным проекциям линий уровня этой плоскости.
На рисунке 8.2 через точку N проведена прямая m, перпендикулярная к плоскости Σ. Для этого в плоскости Σ (а^b) определены горизонталь h и фронталь f, и горизонтальная проекция перпендикуляра проведена перпендикулярно к горизонтальной проекции горизонтали, а фронтальная проекция — перпендикулярно к фронтальной проекции фронтали: 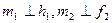 .
.
Действительно, из чертежа следует, что прямая m перпендикулярна к прямой h, так как угол между горизонтальными проекциями сторон угла прямой и одна сторона его (h) параллельна плоскости П1. Точно так же прямая m перпендикулярна к прямой f. Но если прямая линия перпендикулярна к двум пересекающимся прямым плоскости, то она перпендикулярна к этой плоскости.
 |
Рис. 8.2
В том случае, когда плоскость задана следами (рис. 8.3), проекции перпендикуляра располагаются перпендикулярно к одноименным следам плоскости: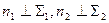 .
.
Плоскость, перпендикулярную к данной прямой, определяют с помощью пересекающихся линий уровня. На рисунке 8.4 (а- условие, 6 - решение) через точку А проведена плоскость 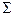 , перпендикулярная к заданной прямой m.
, перпендикулярная к заданной прямой m.
Горизонталь h плоскости проходит через точку А 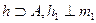 ). Фронталь этой плоскости может быть также проведена через точку А, но может пересекать горизонталь и в любой другой точке, поскольку все они находятся в искомой плоскости.
). Фронталь этой плоскости может быть также проведена через точку А, но может пересекать горизонталь и в любой другой точке, поскольку все они находятся в искомой плоскости.
На рисунке 8.4 фронталь f2 проходит через точку В 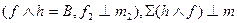 .
.
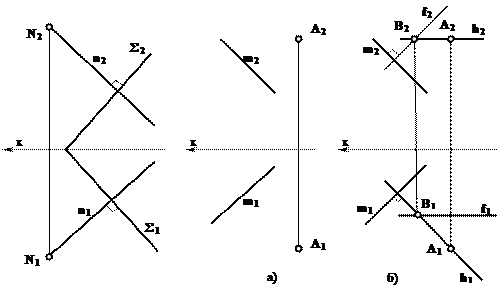
Рис. 8.3 Рис. 8.4
На рисунке 8.4 фронталь f2 проходит через точку В 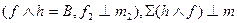 .
.
На рисунке 8.5 показана прямая n перпендикулярная горизонтально проецирующей плоскости. Эта прямая является горизонталью.
На рисунке 8.6 изображена прямая n, перпендикулярная к фронтально проецирующей плоскости. Эта прямая n является фронталью.
На рисунке 8.7 изображен отрезок прямой (MN), перпендикулярный к профильно проецирующей плоскости 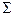 . Заметим, что, проведя проекции М1N1
. Заметим, что, проведя проекции М1N1 Σ1 (Σ1≡h 1) M2N2
Σ1 (Σ1≡h 1) M2N2  Σ2 (Σ2≡f 2) мы еще не определим величину искомого перпендикуляра.
Σ2 (Σ2≡f 2) мы еще не определим величину искомого перпендикуляра.
Это не должно нас удивлять, так как (h≡f), а перпендикулярность прямой и плоскости обеспечивается перпендикулярностью этой прямой к двум пересекающимся прямым плоскости. Для решения задачи нужно построить профильный след. Тогдa M3N3  Σ3 .
Σ3 .
Если требуется определить, перпендикулярна ли некоторая прямая т кзаданной плоскости Σ, то через какую-нибудь точку М этой прямой следует провести перпендикуляр n к плоскости Σ (рис. 8.8). При совпадении линии m и n прямая m перпендикулярна к плоскости Σ.
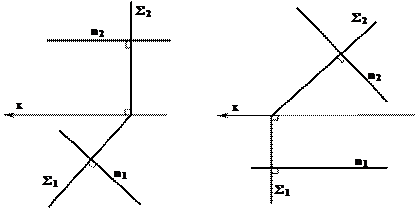
Рис. 8.5 Рис. 8.6
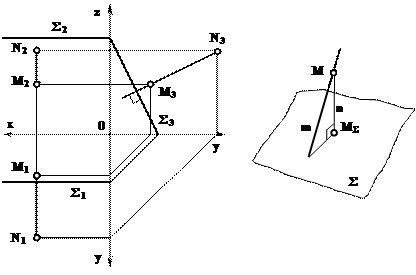 |
Рис. 8.7 Рис. 8.8
|
|
|
|
|
Дата добавления: 2013-12-12; Просмотров: 274; Нарушение авторских прав?; Мы поможем в написании вашей работы!