Сечение многогранников плоскостью

Примеры решения задач

Ниже приведены решения одной и той же задачи вышеописанными методами.

9.6.1. Задание: определить натуральную величину треугольника ABC (рис. 9.8), а также угол наклона плоскости треугольника к плоскости П_{1 .}

1) Решение методом замены плоскостей проекций (рис. 9.9).

Плоскость треугольника спроецируется в натуральную величину в том случае, если она будет параллельна одной из плоскостей проекций. Одним преобразованием задачу решить невозможно. Она решается в два этапа: при первой замене плоскостей проекций получают плоскость треугольника ABC, перпендикулярную к новой плоскости проекций, при второй замене - получают плоскость треугольника, параллельную новой плоскости проекций.

Первый этап. Одним из условий перпендикулярности двух плоскостей является наличие прямой, принадлежащей одной из плоскостей, перпендикулярной к другой плоскости. Используя этот признак, проводят через точку А в плоскости треугольника горизонталь (h). Затем на произвольном расстоянии от горизонтальной проекции треугольника A₁B₁C₁ проводят ось x_1,4 новой системы плоскостей проекций П₁/П₄ перпендикулярно к горизонтальной проекции горизонтали h₁. В новой системе треугольник ABC стал перпендикулярен к новой плоскости проекций П₄.

На линиях проекционной связи в новой системе откладывают координаты z точек А, В, С с фронтальной проекции исходной системы плоскостей П₁/П₂.

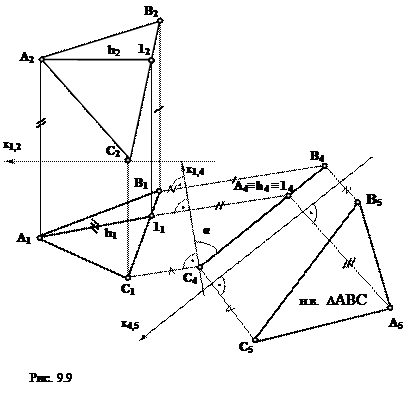
При соединении новых проекций А₄,B₄, С₄ получают прямую линию, в которую спроецировался треугольник ABC. На этом этапе определяется угол наклона плоскости треугольника к горизонтальной плоскости проекции П₁ – угол α. На чертеже это угол между осью x_1,4 и проекцией С₄А₄В₄.

Второй этап. Выбираем новую плоскость проекции П₅, параллельную плоскости треугольника, т.е. новую ось x_4,5 проводят параллельно С₄А₄В₄ на произвольном расстоянии. Получают новую систе­му П₄/П₅. Полученный треугольник А₅В₅С₅ и есть искомая натуральная величина треугольника ABC.

2) Решение методом вращения вокруг проецирующей оси (рис. 9.10).

Задача решается в два этапа. На первом этапе выполняют вращение так, чтобы плоскость треугольника ABC преобразовалась в проецирующую плоскость, т.е. стала перпендикулярна к одной из плоскостей проекций. Для этого проводят горизонталь h (h₁,h₂) через точку А. (построение начинают с фронтальной проекции h₂, она проходит через проекцию точки A₂ и проекцию точки 1₂ при этом h₂ параллельна оси х). Далее находят горизонтальную проекцию h₁ горизонтали h (через проекции A₁ и 1₁). Через точку А проводят ось i - ось вращения треугольника так, чтобы она была перпендикулярна к П₁. На фронтальной проекции через вершины А₂ и В₂ проводят следы горизонтальных плоскостей уровня Δ и Σ в которых при вращении будут перемещаться точки А и В. Вершина С принадле­жит плоскости П₁ поэтому ее плоскостью вращения будет плоскость проекций П₁. На горизонтальной проекции, взяв за центр вращения проекцию i₁ поворачивают горизонталь А так, чтобы на плоскость П₂ она спроецировалась в точку. На чертеже это выразится 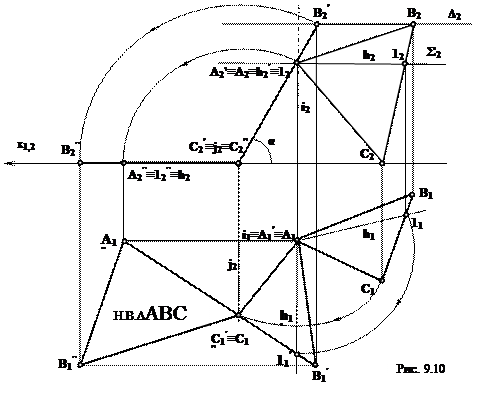тем, что h'₁ займет новое положение - перпендикулярно к оси х.

При этом на фронтальной проекции А₂ остается неизменной, находясь на следе плоскости Σ₂ и ее обозначим a₂'.

На гори­зонтальной проекции поворачиваем оставшиеся вершины В и С во­круг оси i так, чтобы 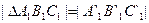. На фронтальной проекции вершина В перемещается по следу плоскости 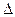₂, а вершина С - по оси х. Соединив новые положения проекций всех вершин треугольника ABC, получают проекцию А'₂В'₂С'₂, сливающуюся в линию. Плоскость треугольника ABC заняла проецирующее положение. На данном этапе, при необходимости, находят угол наклона плоскости треугольника ABC к П₁ – угол α.

На втором этапе проводят ось j через вершину С так, чтобы ось была фронтально проецирующая. При этом С'₂ ≡ j'₂, а горизонтальная проекция j'₁ пройдет через проекцию С'₁. Вокруг оси поворачивают треугольник так, чтобы он стал параллелен горизонтальной плоскости проекций. В данной задаче вращают точки А'₂ и В'₁, вокруг j₂ до совмещения с осью х,при этом проекции B'₁ и A'₁ будут перемещаться параллельно оси х и займут новое положение В"₁, и А"₁ вершина С оста­нется на месте. Соединив точки между собой, получают новое положение плоскости (оно соответствует натуральной величине треугольника ABC).

3) Решение методом плоскопараллельного перемещения (рис. 9.11).

Задача решается в два этапа. На первом этапе преобразуют чертеж так, чтобы плоскость треугольника ABC стала перпендику­лярна к одной из плоскостей проекций. Для этого проводят в плоскости треугольника горизонталь h (фронтальная проекция А₂1₂ ║ х,). Каждую вершину треугольника заключают в свою плоскость уровня, параллельную плоскости П₁. В рассматриваемом примере вершина С принадлежит плоскости проек­ций П₁, А принадлежит плоскости Σ, В — плоскости Δ.

Плоскость треугольника перемещается в пространстве до тех пор, пока горизонталь h₁ треугольника не станет перпендикулярна к фронтальной плоскости проекций П₂.

Для этого на свободном поле чертежа вычерчивают горизонтальную проекцию треугольника A₁^′B₁^′C₁^′ с условием, чтобы А₁1₁ 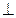П₂, а значит А₁^′1₁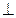^′х. При этом вершины треугольника, перемещаясь каждая в своей плоскости, займут новое положение – (фронтальная проекция А₂В₂С₂ заменится А'₂В'₂С'₂). Соединив эти точки, получают новое положение треугольника ABC, спроецированного в линию, т.е. перпендикулярного к плоскости П₂.

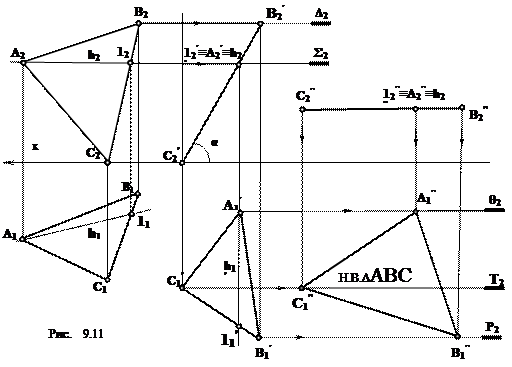
На втором этапе, чтобы получить натуральную величину треугольника ABC, его плоскость поворачивают до тех пор, пока она не будет параллельна одной из плоскостей проекций. В рассматриваемом решении фронтальную проекцию треугольника А₂'В₂'С₂' располагают на произвольном расстоянии от оси х параллельно плоскости П₁. При этом вершины А, В и С треугольника заключают в горизонтально проецирующие плоскости θ, Т, Р. По следам этих плоскостей будут перемещаться горизонтальные проекции вершин А₁'В₁'С₁'. От нового положения фронтальной проекции А₂"В₂"С₂" проводят линии проекционной связи до пресечения с соответствующими следами плоскостей, в которых они перемещаются (θ₁,T₁,P₁), и получая проекции точек А₁" В₁" C₁". Соединив эти проекции, получают тре­угольник ABC в натуральную величину.

4) Решение методом вращения вокруг линии уровня (рис.9.12)

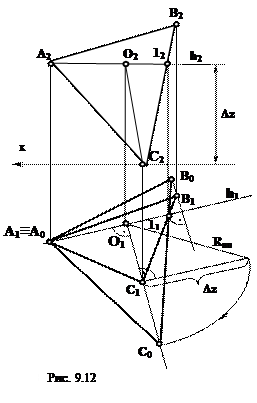Для решения задачи этим способом необходимо повернуть плоскость треугольника вокруг линии уровня, в данном случае вокруг горизонтали, до положения, параллельного горизонтальной плоскости проекции. Через точку А в плоскости треугольника ABC проводят горизонталь h, фронтальная проекция которой будет параллельна оси х. Отмечают точку 1₂ и находят ее горизонтальную проекцию 1₁. Прямая A₁1₁ является горизонтальной проекцией h₁ горизонтали h. Вокруг горизонтали будут вращаться точки В и С. Определяют натуральную величину радиуса вращения точки С.

Для определения натуральной величины радиуса вращения используют любой метод (в данном случае способ прямоугольного треугольника) строят прямоугольный треугольник, в котором O₁C₁ - один из катетов. Вто­рой катет - разность координат Δz отрезка О₂С₂, взятого с фронталь­ной проекции. В построенном треугольнике гипотенуза O₁C₀ - нату­ральная величина радиуса вращения.

На продолжении перпендикуляра O₁C₁ откладывают |R_Bp.| и полу­чают новое положение вершины С после вращения — С₀. Проекция вер­шины В₀ получается пересечением луча C₀1₁ и перпендикуляра к горизонтальной проекции h₁ проведенного через проекцию точки В₁.

Треугольник A₀B₀C₀ есть искомая натуральная величина тре­угольника ABC.

5) Решение методом совмещения (рис. 9.13).

Для решения задачи методом совмещения необходимо построить следы плоскости Σ, которой принадлежит треугольник ABC. Для этого проводят в плоскости треугольника ABC фронталь f и находят горизонтальный след этой фронтали – N₁. По условию задачи вершина С треугольника принадлежит горизонтальной плоскости проек­ций П₁. Тогда горизонтальный след Σ₁ плоскости Σ проводят через проекции N₁ и C₁. Соединив эти две точки и продлив отрезок до пересечения с осью х, находят точку схода следов Σ_х. Учитывая, что все фронтали плоскости параллельны ее фронтальному следу, фронтальный след Σ₂ плоскости Σ проводят через точку Σ_х параллельно проекции фронтали f₂.

Для нахождения натуральной величины треугольника ABC необходимо построить совмещенное положение плоскости Σ с горизонтальной плоскостью проекций П₁. Для этого через вершину А проводят горизонталь h₁. На фронтальном следе Σ₂ фиксируют точку 2₂. Ее горизонтальная проекция - точка 2₁. Точка 2 вращается в плоскости, перпендикулярной к горизонтальному следу плоскости Σ. Поэтому, чтобы построить точку 2 в совмещенном положении 2₀, проводят из 2₁ перпендикуляр к горизонтальному следу Σ, а из центра Σ_х дугу окружности радиусом Σ_х2₂ до пересечения с направлением перпендикуляра. Соединив Σ_х с 2₀, получают совмещенное положение фронтального следа Σ₀ - Далее через точку 2₀ проводят горизонталь h₀ всовмещенном положении. На этой горизонтали находят точку А₀, проведя перпендикуляр из точки A₁ к горизонтальному следу Σ₁.

По такой же схеме строят совмещенное положение точки В₀. Совмещенное положение точки С совпадает с ее горизонтальной проекцией С₁ т.е. С ₁≡ С₀. Соединив построенные точки, получают треугольник А₀В₀С₀ - это и есть натуральная величина треугольника ABC.

1. МНОГОГРАННИКИ.

Дата добавления: 2013-12-12