Параллактический треугольник. Преобразования координат

Теорема о высоте северного полюса мира над горизонтом

Вращение небесного свода — явление кажущееся и представляет собой следствие действительного вращения Земли вокруг оси в направлении, противоположном суточному вращению неба, т.е. с запада на восток. Поэтому в какой бы точке на поверхности Земли наблюдатель ни находился, он всегда видит вращение небесной сферы происходящим вокруг оси мира — прямой, параллельной оси вращения Земли.

Направление же отвесной линии меняется при перемещении наблюдателя по земной поверхности и составляет различные углы с осью вращения. Взаимное расположение кругов и точек небесной сферы, связанных с осью мира и с отвесной линией, зависит, следовательно, от направления последней, т.е. от положения наблюдателя на поверхности Земли.

Эта зависимость формулируется в виде следующей теоремы: «высота северного полюса мира h_P над горизонтом равна географической широте j места наблюдения».

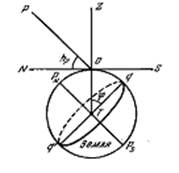
Рис. 1.5. Связь между высотой полюса мира и географической широтой.

Географической широтой точки О (рис. 1.5) называется величина дуги географического меридиана от экватора до точки О. На чертеже P_N и P_S — соответственно северный и южный географические полюсы Земли, q и q¢ — точки земного экватора, T — центр Земли.

Доказательство теоремы следует непосредственно из чертежа, где Ð PON = h_P и Ð OTq= j — углы со взаимно перпендикулярными сторонами.

Многие задачи астрономии, связанные с видимыми положениями и движениями небесных тел, сводятся к решению сферических треугольников.

Сферическим треугольником называется фигура АВС на поверхности сферы, образованная дугами трех больших кругов (рис. 1.6). На чертеже a, b и c —стороны треугольника, R — радиус сферы.

Рис. 1.6. Сферический треугольник.

В сферическом треугольнике и стороны, и углы измеряются в угловых единицах. Сферический треугольник отличается по своим свойствам от плоского, и применять к нему формулы тригонометрии на плоскости нельзя. Для него справедливы следующие теоремы сферической тригонометрии.

Теорема косинусов. Косинус стороны сферического треугольника равен произведению косинусов двух других его сторон плюс произведение синусов тех же сторон на косинус угла между ними:

cos а = cos b cos с + sin b sin с cos A.

(1.3)

Теорема синусов. Синусы сторон сферического треугольника пропорциональны синусам противолежащих им углов:

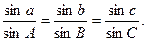
(1.4)

Формула пяти элементов. В сферическом треугольнике произведение синуса стороны на косинус прилежащего угла равняется произведению синуса другой стороны, ограничивающей прилежащий угол, на косинус третьей стороны минус произведение косинуса стороны, ограничивающей прилежащий угол, на синус третьей стороны и на косинус угла, противолежащего первой стороне:

sin a cos В = sin c cos b — cos c sin b cos A.

(1.5)

Параллактическим треугольником называется треугольник на поверхности небесной сферы, образованный пересечением небесного меридиана, круга высоты и круга склонения светила. Его вершинами являются полюс мира Р, зенит Z и светило М.

Если светило М находится в западной половине небесной сферы (рис. 1.7), то сторона ZP (дуга небесного меридиана) равна 90° — j, где j — широта места наблюдения; сторона ZM (дуга круга высоты) равна зенитному расстоянию светила z = 90° — h, где h — высота светила; сторона РМ (дуга круга склонения) равна полярному расстоянию светила р = 90° — d, где d — склонение светила; угол PZM = 180° — А, где A — азимут светила; угол ZPM = t, т.е. часовому углу светила; угол PMZ = q называется параллактическим углом.

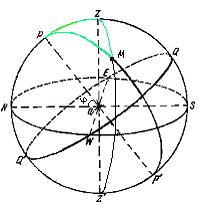
Рис. 1.7. Небесная сфера и параллактический треугольник.

Применяя основные теоремы сферической тригонометрии к параллактическому треугольнику (рис. 1.7), можно получить формулы перехода от одних небесных координат к другим. Так, для случая перехода от горизонтальных координат светила к экваториальным получаем следующие соотношения:

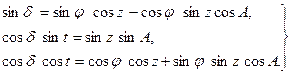
(1.6)

Формулы перехода от одних небесных координат к другим используются при вычислении моментов времени восхода и захода светил и их азимутов в эти моменты, а также при решении двух очень важных задач практической астрономии — определения географической широты места наблюдения j и определения местного звездного времени s.

Дата добавления: 2013-12-12