Определение расстояний в Солнечной системе

Определение расстояний до тел Солнечной системы основано на измерении их горизонтальных параллаксов.

Угол между направлениями, по которым светило М' было бы видно из центра Земли и из какой-нибудь точки на ее поверхности, называется суточным параллаксом светила (рис. 2.3). Иными словами, суточный параллакс есть угол р', под которым со светила был бы виден радиус Земли в месте наблюдения.

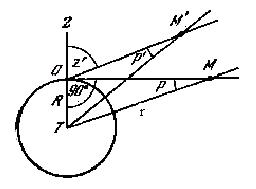
Рис. 2.3. Суточный параллакс.

Для светила, находящегося в момент наблюдения в зените, суточный параллакс равен нулю. Если светило М наблюдается на горизонте, то суточный параллакс его принимает максимальное значение и называется горизонтальным параллаксом р.

Вследствие суточного параллакса светило кажется нам ниже над горизонтом, чем это было бы, если бы наблюдение проводилось из центра Земли; при этом влияние параллакса на высоту светила пропорционально синусу зенитного расстояния, а максимальное его значение равно горизонтальному параллаксу p.

В рамках Солнечной системы расстояния до небесных тел определяются как геоцентрические, т.е. от центра Земли до центра небесного тела. На рис. 2.3 расстояние r до светила М есть TM.

Так как Земля имеет форму сфероида, то во избежание разногласий в определении горизонтальных параллаксов необходимо вычислять их значения для определенного радиуса Земли. За такой радиус принят экваториальный радиус Земли R _Å = 6378 км, а горизонтальные параллаксы, вычисленные для него, называются горизонтальными экваториальными параллаксами. Именно эти параллаксы тел Солнечной системы приводятся во всех справочных пособиях.

Зная горизонтальный параллакс р светила, легко определить его геоцентрическое расстояние. Действительно, если ТО = R _Å есть экваториальный радиус Земли, ТМ = r — расстояние от центра Земли до светила М, а угол р — горизонтальный параллакс светила, то из прямоугольного треугольника ТОМ имеем

.

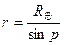(2.8)

Для всех светил, кроме Луны, параллаксы очень малы (у Луны в среднем р = 57', у Солнца р_¤ = =8",79, у планет меньше 1¢). Поэтому формулу (2.8) можно написать иначе, учитывая, что угол р мал и :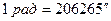

,

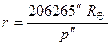(2.9)

где p² — горизонтальный параллакс в угловых секундах. Расстояние r получается в тех же единицах, в которых выражен радиус Земли R _Å.

Горизонтальный параллакс светила можно определить по суточному параллактическому смещению этого светила на небе, которое получается вследствие изменения положения наблюдателя в результате перемещения его по поверхности Земли.

Горизонтальному параллаксу Солнца р_¤ = 8",79 соответствует среднее расстояние Земли от Солнца, равное приблизительно 149,6 × 10⁶ км. Это расстояние в астрономии принимается за одну астрономическую единицу (1 а.е.), т.е. 1 а.е. = 149,6 × 10⁶ км. В астрономических единицах обычно выражаются расстоянии до тел Солнечной системы. Например, Меркурий находится от Солнца на расстоянии 0,387 а.е., а Плутон — на расстоянии 39,4 а.е.

Если большие полуоси орбит планет выражать в астрономических единицах, а периоды обращений планет — в годах, то для Земли а = 1 а.е., Т = 1 год и период обращения вокруг Солнца любой планеты с учетом формулы (2.7) определяется как

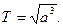
(2.10)

Быстрое развитие радиотехники дало астрономам возможность определять расстояния до тел Солнечной системы радиолокационными методами. В 1946 г. была произведена радиолокация Луны, а в 1957-1963 гг.— радиолокация Солнца, Меркурия, Венеры, Марса и Юпитера. По скорости распространения радиоволн с = 3 × 10⁵ км/с и по промежутку времени t прохождения радиосигнала с Земли до небесного тела и обратно легко вычислить расстояние r до небесного тела по приближенной формуле:

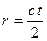
(2.11)

(более точная формула получается в общей теории относительности).

Дата добавления: 2013-12-12