Тема: Системы счисления, используемые в ЭВМ

Ответы на задания.

№10.

Вопросы и задания для контроля полученных знаний.

№9.

№8.

Десятичная система счисления. Современная десятичная позиционная система С. возникла на основе нумерации, зародившейся не позднее 5 в. в Индии.

Марокканский историк Абделькари Боужибар писал, что арабским цифрам в их первоначальном варианте было придано значение в строгом соответствии с числом углов, которые образуют фигуры.

В самом деле, если посмотреть на нижеприведенную схему, это предположение кажется не лишенным смысла.

Так единица создает лишь один угол, тройка – три, пятерка – пять и т.д. Нуль не образует никакого угла, поэтому не имеет никакого содержания.

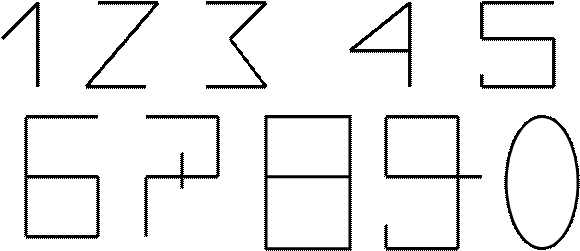
До этого в Индии имелись системы С., в которых применялся не только принцип сложения, но принцип умножения (единица какого-нибудь разряда умножается на стоящее слева число). Аналогично строились старокитайская система С. и некоторые другие. Если, например, условно обозначить число 3 символом III, а число 10 символом X, то число 30 запишется как IIIX (три десятка).Такие системы С. могли служить подходом к созданию десятичной позиционной нумерации. Десятичная позиционная система С. даёт принципиальную возможность записывать сколь угодно большие числа.

Запись чисел в ней компактна и удобна для производства арифметических операций. Поэтому вскоре после возникновения десятичная позиционная система С начинает распространяться из Индии на Запад и Восток. В 9 в. появляются рукописи на арабском языке, в которых излагается эта система С., в 10 в. десятичная позиционная нумерация доходит до Испании, в начале 12 в. она появляется и в других странах Европы. Новая система С. получила название арабской, потому что в Европе с ней познакомились впервые по латинским переводам с арабского. Только в 16 в. новая нумерация получила широкое распространение в науке и в житейском обиходе. В России она начинает распространяться в 17 в. и в самом начале 18 в. вытесняет алфавитную. С введением десятичных дробей десятичная позиционная система С. стала универсальным средством для записи всех действительных чисел.

Десятичная система характеризуется тем, что в ней 10 единиц какого-либо разряда образуют единицу следующего старшего разряда. Другими словами, единицы различных разрядов представляют собой различные степени числа 10.

В десятичной системе используются цифры от 0 до 10. Причём, т.к. система позиционная, положение цифр имеет значение: справа налево разряд увеличивается. Десятичная система наиболее удобная для людей во многом потому, что у нас по десять пальцев на руках и на ногах.

Например, Десятичное число А₁₀=4718,63 в развернутой форме запишется так:

А₁₀=4*10³+7*10²+1*10¹+8*10⁰+6*10^-1+3*10^-2

1. Что такое система счисления?
2. Какие виды систем Вы знаете?
3. Какие виды счисление используются в настоящее время?
4. Какой числовой эквивалент имеет цифра 6 в числах:

1. Сравните числа VVV и 555.
2. Какие числа записаны римскими цифрами:

а) MCMXCIX; б) CMLXXXVIII; в) MCXLVII?

1. Запишите год, месяц и число своего рождения c помощью римских цифр.
2. Некоторые римские цифры легко изобразить, используя палочки или спички. Ниже написано несколько неверных равенств. Как можно получить из них верные равенства, если разрешается переложить с одного места на другое только одну спичку (палочку)?

VII — V=XI IX—V=VI

VI — IX=III VIII - III=X

4. а) 6 тысяч; б) 6 сотен; в) 6 единиц; г) 6 десятков.

5. VVV(5+5+5=15)<555.

6. а) M(1000)CM(1000-100)XC(100-10)IX(10-1)» 1999;

б) 988;

в) 1147.

8. Один из возможных способов решения:

VI + V=XI XI—V=VI

VI =IX—III VIII +II=X

Урок №4.

Цель: Познакомить студентов со системами счисления, применяемыми для кодирования информации в ЭВМ. Научить правилам перевода чисел из одной системы счисления в другую.

Рассматриваемые вопросы:

1. Двоичная система счисления.

2. Восьмеричная система счисления.

3. Шестнадцатеричная система счисления.

4. Правила перевода чисел из одной системы счисления в другую.

5. Перевод двоичных чисел в восьмеричную и шестнадцатеричную системы счисления.

Дата добавления: 2013-12-12