Газы: идеальный и реальный. Статистика Ферми и Бозе для квантовых идеальных газов. Законы излучения абсолютно черного тела(фотонный газ)

Лекция 19-22

1. Используя статическую сумму идеального газа, в которой 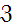заменено на ν – число степеней свободы, имеем:

(1)

Где n=– плотность числа частиц

2. Энергия U и теплоемкость 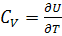. Имеем:

при N=(2)

Теплоемкость 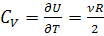(3)

3. Двух атомные газы типа 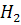, энергия молекулы у них

(4)

Усредняя, получим

(5)

рис. 1.

Теплоемкость в расчете на 1 кмоль имеет вид (см. рис.1)

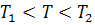
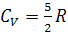При T, при и при

4. Реальный газ, его уравнение состояния.

Рассмотрен в книге(Абрамович Т.М., Донских С.А., Семин В.Н. и др. «Термодинамика и статическая физика. Методы решения задач.», Таганрог, издательство Таганрогского государственного педагогического института, 2004, с. 7-8 и с.52-53).

5. Квантовые идеальные газы. Статистики Ферми и Бозе.

Рассматриваются идеальные газы: электроны в молекулах, фотоны в камере с зеркальными стенам. Постулат квантовой теории: одинаковые частицы принципиально не различимы, т.е. (6)

Отсюда легко показать, что для электронов следует принцип Пауле, т.к. они описываются формулами (полуцелый спин). Частицы с целым или нулевым спином описываются формулами , т.е. на низ запрет Пауле не распространяется.

Статистика электронного газа может быть получена с помощью вариационного принципа для соответствующего термодинамического потенциала. Для электронного газа используется Ω – потенциал для системы с T,

Имеем:

(7)

Получаем

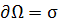(8) для равновесного состояния имеем:

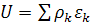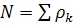, , (9)

Здесь - вероятность заполнения катого квантового состояния, вероятность дырки, т.е учтен принцип Паули.

Из условия мы находим функцию распределения электронов:

(10)

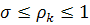
Для бозонов имеем

(11)

Фотонный газ и законы излучения абсолютно черного тела рассмотрены в книге (Абрамович Т.М., Донских С.А., Семин В.Н. и др. «Термодинамика и статическая физика. Методы решения задач.», Таганрог, издательство Таганрогского государственного педагогического института, 2004, с. 9-11).

Лекции 23-26

Введение в курс ФТГ. Адиабатическое приближение. Одноэлектронное приближение. Уравнение Шрединера в одноэлектронном приближении и принципы его решения. Зоны энергии. Металлы. Статистика электронов в Ме. Уровень Ферми. Внутренняя энергия и теплоемкость Ме

1. Сущность адиабативного приближения состоит в том, что в силу относительно медленного движения ядер в кристалле, электроны можно рассматривать независимо, при неподвижных ядрах. Общее уравнение:

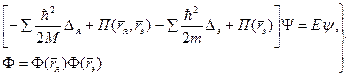(1)

Одноэлектронное приближение - выделяется 1 электрон на фоне полей ядер и остальных электронов; он находится в самосогласованном периодическом поле (периоды решетки кристалла).

Имеем 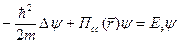(2)

Решение этого уравнения - функции Блоха:

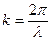, , (3)

- периодическая функция, (4).

2. Решение для энергии имеет структуру зон, что упрощенно иллюстрируется рис. 1. Характеристика зоны для Na. Его валентные электроны заполняют подуровни зоны проводимости на 2 на подуровень (принцип Паули). Наивысший уровень заполненной части зоны - уровень Ферми E_F.

Статистика электронов - статистика Ферми-Дирика; имеем:

(5)

Отсюда находим m, причем . Ширина области, где имеем в зоне полузаполненные состояния

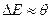. (6)

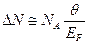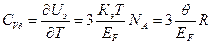Число электронов, участвующих в теплообмене (6a) (мы приняли ). Тогда энергия этих электронов, ели для них использовать классическое распределение: и теплоемкость (7).

Мы видим, что она при температурах много выше Т =0 очень мала и теплоемкость металлов мало отличается от теплоемкости неметаллов.

Дата добавления: 2013-12-12