Простейшие движения твердого тела

Классификация движений точки по ускорению

Определение проекций ускорения на естественные оси при координатном способе задания движения

Ускорение точки при естественном способе задания движения

Ускорение точки при координатном способе задания движения

Ускорение точки при векторном задании движения.

Ускорение точки.

Скорость точки при естественном задании движения.

При использовании естественного способа задания движения точки её положение характеризуется дуговой координатой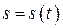. Положение точки в этом случае представляется радиус вектором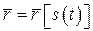. Тогда скорость точки можно определить следующим образом (рис. 1.3):

,

где 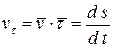— проекция вектора скорости на единичный вектор касательной к траектории .

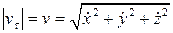Следовательно, вектор скорости направлен по касательной к траектории.

При изучении движения необходимо знать, как быстро меняется скорость по величине и направлению. Векторная величина, характеризующая быстроту изменения скорости, называется ускорением.

Пусть за время 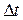скорость изменилась на величину 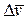(рис.1.4). Тогда средним за это время ускорением имеет смысл назвать величину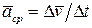. Предел этого отношения при 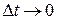характеризует мгновенную скорость изменения скорости, т. е. ускорение

.

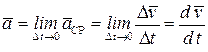Таким образом, ускорение равно производной по времени от вектора скорости.

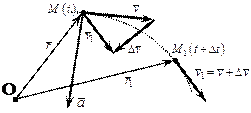
Рис. 1. 4. Ускорение точки

В том случае заданы координаты как функции от времени

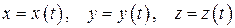
Так как скорость можно разложить на составляющие вдоль координатных осей, то после дифференцирования по времени получим:

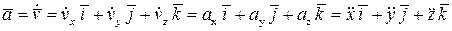
Модуль вектора ускорения и его направляющие косинусы можно вычислить по формулам:

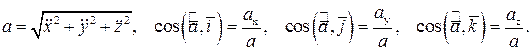
Известна зависимость дуговой координаты S от времени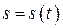. Скорость точки определяется формулой:

.

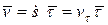Найдём ускорение, продифференцировав это соотношение по времени. Учтём при этом, что единичный вектор касательной 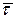меняет направление при движении точки, и он может быть рассмотрен как сложная векторная функция 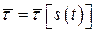. Тогда

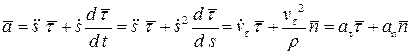
где 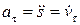— называется касательным (тангенциальным) ускорением, 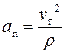— называется нормальным ускорением.

Т. к.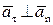, модуль ускорения можно найти по теореме Пифагора:

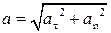
Из изложенного выше следует, что вектор ускорения располагается в соприкасающейся плоскости и направлен в сторону вогнутости траектории. Проекции вектора ускорения на естественные оси равны:

.

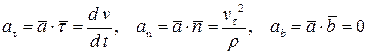Касательное ускорение можно определить следующим образом. Представим единичный вектор касательной в виде 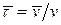. Тогда

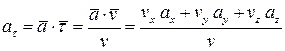
Кроме того, касательное ускорение можно определить, продифференцировав по времени выражение 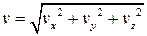, если движение задано координатным способом.

Полное ускорение определяется формулой:.

Нормальная составляющая найдётся из формулы: 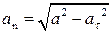, а радиус кривизны: .

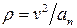Анализируя вышесказанное, можно сделать следующие выводы:

· если 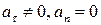, то точка движется прямолинейно;

· если 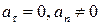, то точка движется равномерно по криволинейной траектории;

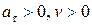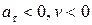· если или , то точка движется ускоренно в сторону возрастания или убывания дуговой координаты соответственно;

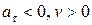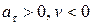· если или , то точка движется замедленно;

· если 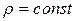, то точка движется по окружности.

Дата добавления: 2013-12-12