Ускорение точки в полярных координатах

Направляющие косинусы ускорения соответственно равны

Модуль ускорения

Проекции ускорения на неподвижные оси координат равны первым производным по времени от соответствующих проекций скорости на те же оси или вторым производным по времени от соответствующих координат движущейся точки.

Откуда

Или

Если движение точки задано координатным способом, т. е. уравнениями

x = x(t), y = y(t), z=z(t),

то, раскладывая векторы r, υ и w по ортам координатных осей, по­лучим

r=ix+jy+kz,

υ= i υ_X +j υ_Y +k υ_Z,

w=i w_X +j w_Y +k w_Z

,где w_X, w_Y,w_Z - проекции ускорения на оси координат. На основании предыдущей формулы можно написать iω_X+i ω_Y+k ω_Z= iυ_X+jυ_Y+kυ_Z

iω_X+i ω_Y+k ω_Z= ix+jy+kz,

ω _х = υ_X = x ω_у = υу = у, ω_Z=υ_Z= z.

ω==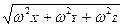

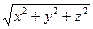
cos(ω^ί)=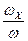; cos(ω^ĵ)=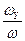; cos(ω^k)=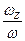

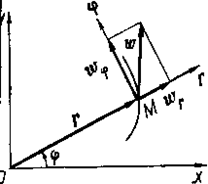
Пусть движение точки М в плоскости Оху задано в полярных координатах г = г (t); φ = φ (t). Декартовы координаты выража­ются через полярные по формулам

х = г соs φ, у = г sinφ..

Найдем проекции ω_r и ω_φ ускорение ω точки на радиальное (r) и трансверсальное (φ) направление (рис.44)

Для ω_X и ω_Y имеем выражение

ω_X=ω_rcosφ-ω_φsinφ, ω_Y=ω_r sinφ+ω_φcosφ

С другой стороны,

ω_Х=x=r cosφ – 2rφ sinφ – rcosφ ∙ φ² – r sinφ ∙ φ,

ω_Y=y=r sinφ + 2 rφ cosφ - rsinφ ∙ φ² + r cosφ ∙ φ

Дата добавления: 2013-12-12