Уравнение Мещерского

При выводе уравнения Мещерского будем исходить из следующих соображений. Пусть точка, масса которой изменяется с течением вре­мени, в момент t имела массу m (t) и абсолютную скорость υ. Тогда количество движения этой точки в момент t равно

k = m(t) υ.

Пусть далее к данной точке за время dt присоединилась другая точка с массой dm (t), обладающая в момент присоединения конечной абсолютной скоростью u.

Тогда в момент t+dt образуется одна точка с массой m (t)+ dm (t), имеющая скорость υ +d υ и количество движения

Поскольку в момент t количество движения указанной системы равнялось m (t) υ + u dm, то приращение количества движения будет равно

С другой стороны, d k = d S, где d S — элементарный импульс равнодействующей силы F. Следовательно,

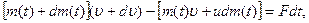
откуда

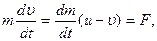
где u — υ = υ _r — относительная скорость присоединенной к точке
массы (рис. 138).
Тогда

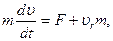
где

называется реактивной силой.

Следовательно,

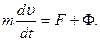
Это дифференциальное уравнение движения точки переменной мас­сы называется уравнением Мещерского. Оно было выведено в его ма­гистерской диссертации, опубликованной в 1897 г.

Основной закон движения точки переменной массы, выражаемый уравнением (111.273). может быть сформулирован следующим обра­зом: при движении точки переменной массы в любой момент времени произведение массы этой точки на ее ускорение равно геометрической сумме действующих на точку сил F и реактивной силы Ф.

Если относительная скорость υ _r= u — υ отделяющихся (или присоединяющихся) частиц будет равна нулю, т. е. тело переменной массы не отбрасывает отделяющиеся от него частицы, а просто распа­дается, то реактивная сила в этом случае будет равна нулю и из урав­нения Мещерского (111.310) видно, что движение такой точки пере­менной массы выражается уравнением

m υ = F,

которое имеет вид уравнения движения материальной точки постоян­ной массы, в котором масса m точки будет переменной величиной, заданной функцией времени.

Проектируя обе части уравнения (111.310) на оси неподвижной системы координат Охуz, получим три скалярных уравнения:

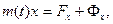
Для подавляющего числа случаев современной ракетодинамики можно принять гипотезу Циолковского, заключающуюся в том, что вектор относительной скорости υ _r отбрасываемых частиц постоянен по величине, лежит на касательной к траектории движения точки переменной массы и направлен в сторону, противоположную вектору скорости v движения излучаемой точки переменной массы, т. е.

υ _r=- υ _r τ _r

где

υ _r==const,

τ — единичный вектор касательной к траектории движения точки переменной массы.

В этом случае уравнение движения (111.310) примет вид

mυ= F - υ _rm(t) τ.

В современной ракетодинамике большой интерес представляет случай прямолинейного восходящего движения ракеты, когда в урав­нении (111.310) равнодействующая внешних сил F представляет собой векторную сумму двух сил F ₁+ F ₂. Сила F ₁ = mа пропорциональна переменной массе движущейся точки; сила F ₂ — сила сопротивления, зависит от скорости движения точки. Эта задача впервые была по­ставлена и частично изучена И. В. Мещерским для двух случаев: когда сила сопротивления F ₂ является линейной функцией скорости точки и когда F ₂ пропорциональна квадрату скорости ее движения. Уравнение (111.311) при F = F ₁ + F ₂, F ₁ = mа примет вид

m υ =m а — υ _rm τ + F ₂.

Если пренебречь силами сопротивления F ₂ и представить массу тела в виде m = m₀ ƒ (t), где m₀ — масса точки вначале, т. е. при t = 0; ƒ (0) = 1, то это уравнение примет вид

где a — известная функция, зависящая как от времени t, так и от расстояния.

В настоящее время функцию ƒ (t) в большинстве случаев принимают при линейном законе изменения массы в виде

ƒ (t)= 1 — αt,

а при показательном законе изменения массы в виде

ƒ (t)=e^-αt.

Таким образом, массу движущейся точки выражают в двух видах:

m(t)= m₀(1 — αt),

m(t)= m₀ e^-αt.

В этом случае реактивная сила Ф = υ _rm будет равна

Ф ⁽¹⁾= - α m₀ υ _r

либо

Ф ⁽²⁾= - α m₀ e^-αt υ _r.

Так как по гипотезе К. Э. Циолковского υ _r = соnst, то величина реактивной силы Ф ⁽¹⁾ будет постоянной, а силы Ф ⁽²⁾ — переменной, уменьшающейся по тому же закону, что и масса движущейся точки.

Таким образом, ускорение 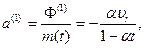вызванное

силой Ф ⁽¹⁾, действующей на точку, переменной массы, будет стечением

времени численно возрастать, а ускорение 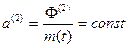бу­дет оставаться постоянным.

Если F = 0, то υ = υ ₀. Отсюда получаем закон инерции для точки переменной массы.

Когда отсутствуют внешние силы, точка переменной массы будет двигаться прямолинейно и равномерно со скоростью υ ₀ (при υ ₀≠ 0) или находиться в покое (при υ ₀= 0), если относительная скорость отделения ее частиц равна нулю, т. ё. υ _r = 0.

Если F = 0 и абсолютная скорость отделяющихся частиц и так­же равна нулю, т. е. при υ _r = — υ получим

m υ= - υ m, или 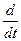(m υ)=0.

Интегрируя и обозначая постоянную интегрирования С = m₀ υ ₀,

получим m υ = m₀ υ ₀, откуда

где m₀ и υ ₀ — масса точки и скорость ее в момент t = 0, принятый за начальный.

Видим, что при отсутствии внешних сил и абсолютной скорости отделения частиц, равной нулю, скорость υ излучающей точки переменной массы увеличивается обратно пропорционально умень­шению массы излучаемой точки.

Дата добавления: 2013-12-12