Этап 2. Синтез приоритетов

Это один из способов решения проблемы многокритериальности. Синтез приоритетов (СП) – это вычисление собственных векторов, которые после нормализации и являются векторами приоритетов. Собственные вектора искать сравнительно трудоемко, поэтому достаточно близкие оценки можно получить с помощью геометрического среднего, для чего элементы каждой строки перемножаются и из результата извлекается корень n-й степени.

Например, для Кр1 в матрице целей:

Кр1: 1*1/2*1/3*1/4*4*3 = ½ Þ ,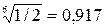

Кр2: 2*1*1/2*1/3*1/4*1/4 = 0,0417 Þ ,

Кр3: 3*2*1*1/3*1*1/2 = 1 Þ ,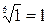

Кр4: 4*3*3*1*1*1/2 = 18 Þ ,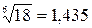

Кр5: ¼*4*1*1*1*1 = 1 Þ ,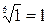

Кр6: 1/3*4*2*2*1*1 = 16/3 Þ .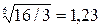

Далее оценки нормируются: ;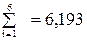

α₁ = 0,917 / 6,193 = 0,148; α₄ = 1,435 / 6,193 = 0,23;

α₂ = 0,616 / 6,193 = 0,1; α₅ = 1 / 6,193 = 0,16;

α₃ = 1 / 6,193 = 0,16; α₆ = 1,23 / 6,193 = 0,198.

Далее для каждого из домов рассчитываются критерии:

Критерий Кр1 дает:

для А: ,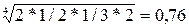

для В: ,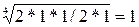

для С: ,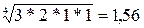

для D: .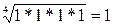

Сумма равна 0,76 + 1 + 1,56 + 1 = 4,32, поэтому:

.

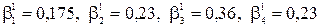Приоритеты получаются путем умножения полученных векторов на соответствующие матрицы:

.

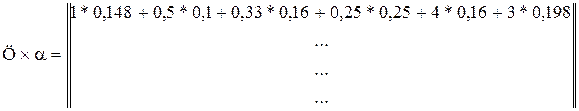Далее оценивается согласованность локальных приоритетов. Для этого используется индекс согласованности (ИС) и отношение согласованности (ОС):

,

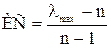где n – число сравниваемых элементов, l_max - максимальное собственное значение матрицы суждений (Ц, Кр1, Кр2…), l_max ³ n:

.

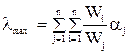ОС = ИС / СС,

где СС – случайная согласованность, определяемая по таблице 5.6.

Таблица 5.6.

n
СС	0,58	0,9	1,12	1,24	1,32	1,41	1,41	1,49

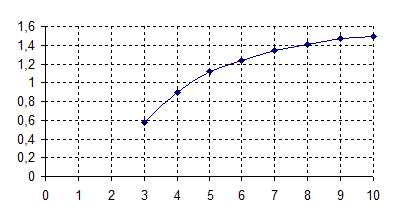
Рис. 5.4.

Должно быть ОС £ 0,1…0,2, иначе следует пересмотреть матрицу суждений.

5.8. Группа методов решения сложных экспертиз.

Как было видно в методе анализа иерархий синтез приоритетов более высокого уровня в отношении вариантов самого низкого уровня проводится по соотношению:

b_(m´1) = A_(m´n) ´a_(n´1),

где A_(m´n) – матрица приоритетов нижнего уровня по отношению к приоритетам верхнего уровня; a_(n´1) – приоритеты критериев; b_(m´1) – приоритеты высшего уровня; m – число вариантов нижнего уровня; n – количество критериев.

Эта идея реализуется в методе решающих матриц:

,

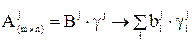где g^j – приоритеты.

Если начать снизу, с задания матрицы предпочтений и приоритетов целей (i + 1) уровня …

Матрица целей: Ц⁰ = А^1.А^2. … А^h.gⁿ.

В отличие от метода анализа иерархий назначение приоритетов на каждом уровне проводится многокритериальным, а не парным сравнением, что требует большей информированности эксперта.

Метод дерева целей еще менее формализован, чем предыдущий.

Существует несколько типовых схем сложных систем принятия решений.

Методы АИ и РМ относятся к так называемым ромбовидным структурам. Для ромбовидной структуры характерно наличие зависимостей целей (i + 1) уровня от одних и тех же элементов i-го уровня (см. рис. 5.5).

Рис. 5.5.

Метод дерева целей, как следует из его названия, не может использоваться для задач подобного вида, что является большим ограничением метода. В то же время, очень большая выразительность и простота метода, являющего методом когнитивной структуризации для большого круга практических задач, сделали его достаточно употребительным (рис. 5.6).

Рис. 5.6.

Идея метода дерева целей:

1) Рисуется структура, отражающая взаимодействие целевых функций между элементами различных уровней.

2) Для каждой связи назначаются веса элементов нижнего уровня для целей верхнего уровня. Веса на каждом уровне должны быть нормализованы.

5.9. Группа экспертных методов.

Отличие экспертных методов от всех предыдущих заключается в том, что помимо формирования процедуры принятия решений при известных предпочтениях эксперта ставится задача формирования и оценки правильности экспертных весов. Известны следующие экспертные методы:

- метод Дельфы (наиболее формализованный),

- метод анкетирования,

- метод дискуссии,

- метод интервьюирования,

- метод сценариев,

- метод «мозгового штурма» и т.д.

Метод Дельфы включает следующие этапы:

1 этап. Выбор группы координаторов (штаба).

2 этап. Выбор группы экспертов, т.е. лиц, принимающих решения (ЛПР).

3 этап. Составление анкет экспертов: вопросы анкеты формируются, исходя из целей координаторов. Например: 1) практический опыт решения аналогичных задач, 2) уровень образования, 3) возраст и т.д.

4 этап. Состав вопросника с указанием числовых критериев ответов- 1-ый тур: 1) факторы, влияющие на выбор и вес фактора; 2) перечень претендентов.

5 этап. Обработка ответов. Каждый эксперт отвечает на эти вопросы и обосновывает свое решение. Далее – выделение группы решений-претендентов на выход в следующий тур.

6 этап. Составление вопросников 2-го тура.

7 этап. Составление сводок, статистическая обработка, вычисление веса каждого варианта, нахождение медиана (среднего арифметического решения) и квартили.

8 этап. Обоснование ответов экспертами, попавшими в 1-ый и 2-ой квартили.

9 этап. Вопросник третьего тура и повтор 7-го и 8-го этапов. Критерий окончание процедуры – отсутствие разногласий во мнениях экспертов, оцениваемая по дисперсии ответов.

В основу метода Дельфы положено следующие положения:

1) ставящиеся вопросы допускают возможность численного оценивания вариантов;

2) ответ на вопрос обосновывается экспертом;

3) ответы должны базироваться на достаточном объеме информации, которая может быть слабо формализованной.

Обработка анкет состоит в том, что оценки экспертов разбиваются на квартили, т.е. на интервалы, примерно равные четверти мнений от числа экспертов.

Квартиль – одна из числовых характеристик распределения вероятностей. Если взять некоторую случайную величину Х, мнения экспертов от 0 до 1 с функцией распределения F(Х) – вероятность соответствующего Х, то квартилью порядка Р называется число К такое, что F(К_р) < Р, F(К_р + e) ³ Р, e ® 0. То есть, квартиль – это мнение каждой четверти экспертов.

Например, мнение каждого эксперта Х Î [0, 1], тогда выделяется примерно четверть экспертов, которые утверждают, что величина Х Î [Х₁, Х₁⁺]. В результате опроса формируется плотность распределения мнений в виде ступенчатого графика или непрерывной кривой. Общее число экспертов упорядочивается по оси Х и разбивается на четыре группы. Мнения крайних групп экспертов обосновываются и озвучиваются. После этого начинается новый тур, эксперты вновь опрашиваются, и можно ожидать, что плотность ответов становится более определенной и интервал разбросов уменьшится.

Близким к методу Дельфы является Дельфийское совещание. Отличие данного метода: обработка анкет не проводится численно, а мнение экспертов просто озвучивается.

Метод дискуссии заключается в обмене мнениями, но решение принимает ЛПР.

Метод «мозгового штурма»: собирается группа лиц из разных областей и каждый высказывается по данной проблеме, при этом критика запрещена. Может оказаться, что какое-нибудь абсурдное мнение окажется правильным.

Синетика – генерирование решений (альтернатив) на основе ассоциативного мышления. Метод аналогичен «мезговому штурму», но подбираются специалисты с ассоциативным характером мышления и обладающие психологической совместимостью. Обсуждение ведется в режиме свободной дискуссии.

Метод сценариев заключается в составлении некоторых деревьев, отражающих причинно-следственные связи между посылами и результатами. Обычно составляются три сценария: пессимистический (для наихудших условий), оптимистический и наиболее вероятный.

Анкетирование и интервьюирование относятся к субъективным методам принятия решений.

5.10. Игровые методы принятия решений.

Игровые методы принятия решений рассматривают вопросы принятия решений в условиях:

1) конфликтного взаимодействия элементов системы,

2) неопределенности,

3) сложности задачи принятия решений, вызванной многообъектностью системы.

Существует пять принципов конфликтного взаимодействия:

1) антагонизм,

2) бескоалиционное взаимодействие,

3) коалиционное взаимодействие,

4) кооперативное взаимодействие,

5) иерархическое взаимодействие с правом первого хода сверху.

Стабильно-зависимое решение в зависимости от постановки задачи бывает:

1) скалярным Нэш-равновесием,

2) векторными равновесиями,

3) угрозы – контругрозы (УКУ),

4) векторно-оптимальное решение,

5) дележ по Шекли.

Для решения всех задач имеются соответствующие алгоритмы.

Наиболее простой случай ситуаций, для которых имеется неопределенность – это случай конфликтных ситуаций, когда сталкиваются противоположные интересы двух или более групп. Выигрыш каждой стороны зависит от поведения соперника, а оно неизвестно.

Теория игр – математическая теория конфликтных ситуаций. Ее цель – дать инструмент для выработки разумного поведения участников конфликта.

Игра ведется по правилам, т.е. должны быть указаны права и обязанности участников. Игра может быть парной и множественной.

Каждый участник делает ходы, которые могут быть личные и случайные. Некоторые игры (часто азартные) не являются предметом теории игр. Если ходы число случайные, то это предмет для теории вероятности.

Если существуют правила вида «если ситуация А, то я поступлю В», значит принята стратегия игры. В зависимости от числа стратегий могут быть конечные и бесконечные игры.

Оптимальной называется стратегия, которая обеспечивает максимальный выигрыш. Если есть случайные ходы, то говорят о максимизации выигрыша в среднем.

Игра называется игрой с нулевой суммой, если алгебраическая сумма выигрыша всех участников равна нулю. самая простая игра с нулевой суммой называется антагонистической (игра со строгим соперником). Теория таких игр наиболее развита и строга.

Рассмотрим игру G с игроками А и В. Будем считать, что «мы» - это А, а противник – В. Пусть у нас имеются m возможных стратегий А_i, а у противника – n стратегий B_j, то есть игра будет (m´n).

Обозначим выигрыш А через a_ij, где i - стратегия А, j – стратегия В. Предполагается, что для всех пар стратегий А_i и В_j выигрыш a_ij известен (а значит, проигрыш В также известен a_ij = - b_ij). Представим информацию в виде таблицы 5.7.

Таблица 5.7.

	В1	В2	…	Вn
А1	a11	a12	…	a1n
А2	a21	a22	…	a2n
…	…	…	…	…
Аm	am1	am2	…	amn

Игра приведена к матричной форме. Обозначим эту матрицу как L = {a_ij}.

Если цифры в строках одинаковые – стратегии называются дублирующими. Можно упростить матрицу, если в ней имеются дублирующие и доминирующие стратегии как по строкам, так и по столбцам путем отбрасывания таких стратегий.

Можно показать, что решение игры сводится к задаче линейного программирования:

L_A = x₁ + x₂ + … + x_m ® min

при ограничениях вида

a₁₁^.x₁ + a₂₁^.x₂ + … + a_m1^.x_m ³ 1

a₁₂^.x₁ + a₂₂^.x₂ + … + a_m2^.x_m ³ 1

a_1n^.x₁ + a_2n^.x₂ + … + a_mn^.x_m ³ 1

при выборе стратегии А^*.

Выбор стратегии В аналогичен, но L_B ® max при выборе стратегии В^*.

Пара задач линейного программирования, по которой находится решение (А^*, В^*) называется двойственной. Показано, что минимум одной линейной функции соответствует максимуму другой.

Рассмотрим пример G(4´5) (см. табл. 5.8). Если мы выберем максимально выигрышную стратегию А₃ (до 10), то противник выберет В₃ и выигрыш будет всего 1. Отсюда типичный принцип игры: минимальный выигрыш должен быть максимальным (принцип минимакса).

Добавим к табл. 5.8 столбец a_i и строку b_j, в которые выпишем минимальные выигрыши для столбца и максимальные для строки.

Таблица 5.8.

	В1	В2	В3	В4	В5	ai
А1
А2
А3
А4
bj

Противник выбирает стратегию, где его проигрыш минимален. Таким образом, исходя из принципа осторожности мы будем выбирать А₄, а противник В₃.

Теперь предположим, что мы узнали о том, что противник выбрал В₃, тогда мы выбираем А₁ и получаем выигрыш 5. Но если противник узнал, что у нас А₁, он выберет В₄ и наш выигрыш будет 2. Мы и противник начали метаться. Это очень важно: минимаксные стратегии неустойчивы по отношению к информации о поведении другой стороны.

Иногда минимаксные стратегии дают устойчивое решение, когда a = b. Стратегии А_i и В_j, дающие на пересечении a = b, называются чистыми, а квадрат матрицы, соответствующий таким стратегиям – седловой точкой матрицы.

5.11. Имитационное моделирование.

Имитационное моделирование (ИМ) имеет целью не только проверку решений, но и их генерирование на основе дуальной процедуры моделирования и разработки модели. Характерной особенностью ИМ является итеративный характер формирования модели объекта и модели принятия решений. ИМ позволяет решать следующие задачи:

1) проверка принимаемых решений,

2) формирование адекватных моделей объектов,

3) оптимизация решений на управление,

4) техническая и психологическая подготовка операторов к решению сложных задач (задача разработки тренажеров-имитаторов).

Структура имитационной системы (ИС) состоит из модели объекта, модели вычисления показателей качества и эффективности (ПКиЭ), блока инициализации управления (ИУ), блока формирования интенсивности управления (ФИУ), блок интерфейса (MMI – Man-Machine Interface, человеко-машинный интерфейс).

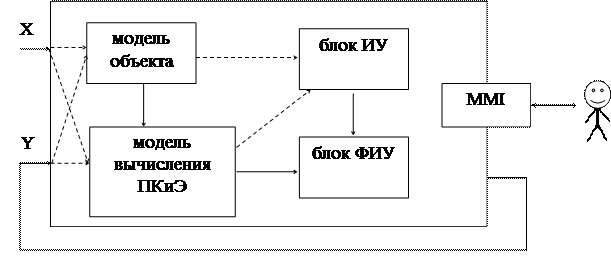
Рис. 5.7.

На рис. 5.7. обозначены параметры: Х – возмущение (воздействие окружающей среды, может быть, модель внешней среды), Y – некоторое управляющее воздействие на объект управления.

Общая идеология использования и создания ИС состоит в том, что построение системы, выбор моделей, проведение экспериментов – это итерационный процесс. Модели элементов усложняются и уточняются на основе анализа чувствительности свойств (характеристик) системы.

Как правило, модели формируются в терминах «вход-выход» и изображаются на топологической уровне в виде функциональных блоков, имеющих наборы входных и выходных координат. Такой подход используется в ряде программных пакетов имитационного моделирования: VisSim, СИАМ, DinSim, Simulink (MatLab) и др. Отличительной чертой этих пакетов является возможность для большинства задач избежать необходимости программирования стандартных для моделирования функций и процедур.

Дата добавления: 2013-12-12