Расчет СМХ методом угла отсечки

Статическая модуляционная характеристика

(СМХ).

СМХ –это зависимость амплитуды 1-ой гармоники выходного тока I₁ модулятора от напряжения смещения E при амплитуде вч несущей U_m=const и амплитуде нч модулирующего сигнала V_m = 0.

1.Аппроксимируем ВАХ отрезками прямых.

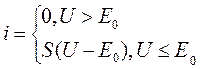S<0;

i

E0 u Рис.7.8.

2. Определяем пределы изменения смещения E.

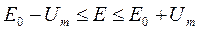
U_m – амплитуда несущей.

3. Задаёмся напряжением смещения Е^/.

4. Определяем угол отсечки:

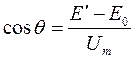
5. Определяем амплитуду первой гармоники:

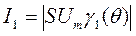, где g₁(q)-коэффициент Берга (см. учебник[1])

6.Возвращаемся в пункт 3 и т.д.

Стандартный вид СМХ показан на рис. 7.9.

Рассмотрим выбор рабочего режима по СМХ.

I₁ I1

I1max

рт I10

I₁min

Emax Eрт Emin E t

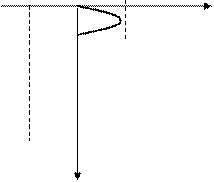Рис.7.9.

uнч

t

1. Выбираем линейный участок (на глаз).

2. Определяем Е_min, E_max, I_max, I_min.

3. Выбираем рабочую точку в середине линейного участка Р.Т.(I₁₀;Е_{Р. Т.})

4. Определяем максимальную амплитуду модулирующего сигнала для неискажённой модуляции:

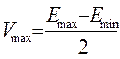
5. Определяем максимальную глубину амплитудной модуля-

ции для неискажённых АМ:

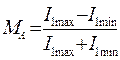
Рассмотрим спектры АМ сигналов при более сложных модулирующих сигналах.

Для простейшего случая, когда модулирующий сигнал представляет собой моногармоническое колебание, спектр модулирующего сигнала показан на рис.7.3 и спектр АМ сигнала на рис.7.4.

Пусть модулирующий сигнал содержит две частоты W₁ и W₂.

Если спектр модулирующего сигнала более сложный, то усложняется спектр АМ сигнала: он содержит спектр модулирующего сигнала, перенесённый на частоту 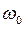, несущую частоту 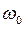и зеркальное отражение спектра модулирующего сигнала относительно несущей.

Спектр модулирующего сигнала.

U

Рис.7.10.

W₁ W₂ w

Спектр АМ сигнала.

u U_m

Дата добавления: 2013-12-12