Термодинамическая вероятность

5.5.3.1. В равновесии термодинамические параметры системы постоянны, но микрохарактеристики молекул претерпевают непрерывные изменения. Таким образом, макросостояния системы реализуется множеством микросостояний. Число микросостояний, совместимых с данным макросостоянием, называется термодинамической вероятностью

5.5.3.2. Принципы расчета термодинамической вероятности.

5.5.3.2.1. Микросостояния отличаются друг от друга перестановкой частиц.

5.5.3.2.2. Перестановки внутри одной ячейки не ведут к новому микросостоянию, так как состояния внутри ячейки неразличимы.

5.5.3.2.3. В одно макросостояние входят все микросостояния с одинаковым количественным распределением частиц по ячейкам, т.е. задать макросостояние на микроуровне можно определением числа частиц в каждой ячейке фазового пространства N_i.

5.5.3.2.4. Основной постулат – для изолированной системы (U= const): все S ^N

микросостояний имеют одинаковую вероятность, т.е. функция распределения r = const. Это позволяет легко рассчитывать термодинамическую вероятность состояния системы, состоящей из N частиц, распределенных по s ячейкам фазового пространства, используя формулу комбинаторики для числа перестановок:

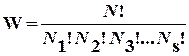, (6.2)

Пример: 2 частицы в двух ячейках (микросостояниях), N = 2, S = 2.

1, 2
			1, 2

4 микросостояния (2²) разбиты на 3 макросостояния:

N1	N2	W

5.5.3.3. Наибольшая термодинамическая вероятность получается при равномерном распределении N частиц по ячейкам с одинаковой энергией.

. (6.3)

С увеличением числа частиц термодинамическая вероятность равномерного распределения частиц по ячейкам очень сильно возрастает

N S W_max

2 2 2

4 2 6

6 3 15

15 3 756756

5.5.3.4. Направление самопроизвольных процессов. Изолированная термодинамическая система стремится к состоянию с наибольшей термодинамической вероятностью, которое достигается при установлении равновесия.

5.5.4. Связь энтропии с термодинамической вероятностью предложена на основании свойств энтропии и термодинамической вероятности

Аддитивность энтропии S = f(W); S = S₁ + S₂.

Мультипликативность термодинамической вероятности W = W₁*W₂.

S(W) = S(W₁*W₂) = S₁(W₁) + S₂ (W₂) Þ S = k ln W, (6.4)

где k – постоянная Больцмана.

Таким образом, энтропия характеризует неупорядоченность системы, ее беспорядок.

Дата добавления: 2013-12-12