Степени свободы. Обобщенные координаты

Л Е К Ц И Я № 7. Т В Е Р Д О Е Т Е Л О В М Е Х А Н И К Е

Положение точки в пространстве можно задать некоторым числом независимых координат, например, тремя координатами х, у, z декартовой системы. Но это можно сделать и иначе. Например, вместо прямоугольных можно взять цилиндрические r, z, j или какие-либо другие координаты. Существенно, однако, что при любом выборе системы координат число независимых координат, требующихся для однозначного определения положения точки, которая может перемещаться в пространстве как угодно, равно трем. Про такую точку говорят, что она обладает тремя степенями свободы.

Пусть материальная точка все время вынуждена находиться на какой-либо заданной поверхности. В этом случае независимыми остаются две координаты, например, х и у. Третья координата может быть вычислена из уравнений связи f(х,у,z) =0. В таких условиях точка обладает двумя степенями свободы.

Если точка может перемещаться только вдоль какой-либо заданной кривой, то число независимых координат, требующихся для определения ее положения, снижается до одного. За координату можно принять, например, расстояние материальной точки от фиксированной точки на кривой, отсчитанной вдоль этой кривой. В таких случаях говорят, что точка обладает одной степенью свободы.

В случае механической системы из n материальных точек, которые могут перемещаться без всяких ограничений, для определения их мгновенного положения надо задать 3 п координат. В этом случае говорят, что система обладает 3п степенями свободы.

Часто свобода перемещения материальных точек ограничена. На 3 п координат налагаются дополнительные условия, называемые связями. Для однозначного определения положения всех материальных точек системы достаточно знать меньшее число координат. Обозначим его через f. Остальные 3 п – f координат могут быть вычислены из уравнений связи.

В качестве независимых координат могут быть использованы любые величины любой размерности

,

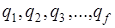заданием которых положение материальных точек системы определяется однозначно. Такие величины называются обобщенными координатами. Обобщенные координаты могут быть выбраны как угодно, лишь бы они в любой момент времени полностью определили положение механической системы. Однако число независимых обобщенных координат f во всех случаях будет одно и то же, и оно равно числу степеней свободы системы.

Дата добавления: 2013-12-12