Вязкость жидкости

Следствия из уравнения Бернулли.

При выводе уравнения Бернулли нами использовался тот факт, что жидкость является идеальной и не сжимаемой, однако в случае если вязкость жидкости будет мала, а плотность также будет мало меняться при переходе от точки к точке, то уравнение Бернулли можно применить при описании реальных жидкостей. Которые отвечают выше изложенным требованиям. В частности в помощью уравнения Бернулли можно построить технологию измерения скорости жидкости текущей в канализационной системе имеющей разные диаметры.

Если ток жидкости находится на одном уровне относительно начала отсчёта (горизонтальный ток), то:

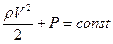
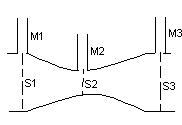
Измеряем давления в разных точках данного тока и применяем уравнение Бернулли определяем скорость действующая там где площадь поперечного сечения будет меньше. Скорость течения жидкости будет больше линии тока будут гуще.

Там где сечение горизонтального тока больше скорость будет меньше. Увеличение скорости ведёт к уменьшению статического давления.

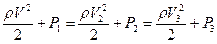
Уравнение Бернулли лежит в основе водоструйного насоса.

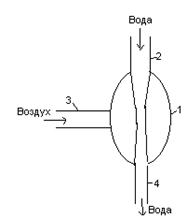
Внутри камеры 1 находится трубка 2 сужающаяся к низу в которую поступает вода а через раструб 3 поступает воздух. За счёт сужения трубки 2 происходит уменьшение давления в области раструба. Благодаря этому вода вместе с воздухом выходит через трубку 4 и нагоняя воду через трубку 2 можно откачать воздух или другой газ из камеры 1.

В реальности жидкость обладает вязкостью. Вязкость – это свойство реальной жидкости оказывать сопротивление перемещению одной части жидкости относительно другой. Силы внутреннего трения направлены по касательной к поверхности перемещающихся слоёв, причём данная сила направлена в сторону препятствующей движению более быстрого слоя, а следовательно в сторону со направленную с движением более медленного слоя.

Сила вязкости возникает тогда, когда имеется изменение (градиент) скорости в направлении перпендикулярном скорости.

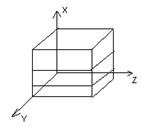
Выберем некоторый объём жидкости изображённый в виде параллелепипеда. Разобьем её на слои. Каждый слой движется с какой то скоростью. Таким образом в направлении оси X (направлении перпендикулярном скорости) имеется изменение скорости жидкости или как говорят градиент скорости. Сила трения между слоями жидкости может быть определена следующим образом:

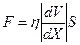
где: η – вязкость жидкости; S – площадь соприкасающихся слоёв.

Вязкость определяется физическими и химическими свойствами жидкости с увеличением температуры у жидкости вязкость уменьшается, а у газов увеличивается.

Течение жидкости можно условно разделить на 2 вида: ламинарное и турбулентное (вихревое). Ламинарным называется такое течение если линии тока остаются постоянными вдоль всего потока и слои жидкости не перемешиваются друг с другом. При турбулентном течении имеются составляющие вектора скорости в слоях жидкости. Нормальные по отношению к границам слоёв. Благодаря этому происходит проникновение частиц жидкости из одних слоёв в другие и взаимное перемешивание.

Ламинарное течение наблюдается при небольших скоростях. Турбулентное при больших. При ламинарном течении профиль вектора скорости в продольном сечении трубки тока жидкости. Он меняется так: вектор скорости принимает максимальное значение в близи средней линии тока. Минимальное значение равное нулю скорость жидкости принимает вблизи стенок трубки тока.

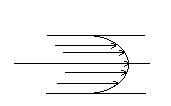
При турбулентном течении изменение скорости по продольному сечению значительно меньше.

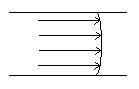
Дата добавления: 2013-12-12