Магнитное поле

Опыт показав что подобно тому как в пространстве окружающем электрические заряды возникает электрическое поле. В пространстве окружающем токи и постоянные магниты возникает магнитное поле. Наличие магнитного поля может быть обнаружено по силовому воздействию на электрические токи (на движущиеся электрические заряды) и на постоянные магниты. Таким образом не смотря на свое электрическое происхождение данный вид силового поля принципиально отличается от электрического поля. Если электрическое поле как генерируется (создается) подвижными и не подвижными электрическими зарядами и может быть обнаружено по силовому воздействию таким образом магнитное поле создается только движущимися электрическими зарядами или связными магнитными зарядами и может быть обнаружено по силовому воздействию на движущийся электрический (связный) магнитный заряд. Характер действия магнитного поля на электрический ток (система движущихся электрических зарядов) определяется конфигурацией проводника по которому протекает данный электрический ток и ориентацией данного проводника во внешнем магнитном поле. С целью упрощения записей и расчётов электрических характеристик проводника находящегося во внешнем магнитном поле вводят специальную характеристику данного проводника – магнитный момент.

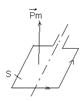Эта векторная величина определяется:

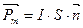
S – площадь поверхности охваченной контуром с током I. 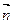- нормаль к данной поверхности.

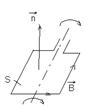Направление нормали определяется в соответствии с правилом правого винта. В том случае если рамку с током закрепить возле некоторой оси по ней пропустить ток и поместить во внешнее магнитное поле, то как показывает эксперимент данная рамка начинает вращаться. Причём механический момент данной рамки, магнитный момент и вектор индукции 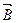магнитного поля связаны между собой с помощью следующего соотношения.

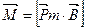
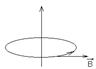
В качестве устройств создающих магнитное поле в электрических цепях часто используют проводники с током так в частности прямолинейный проводник создает вокруг себя магнитное поле, линии индукции охватывают данный проводник причём направление силовых линий магнитного поля может определяться в соответствии с правилом правого винта: Если винт с правой нарезкой вращать так что поступательное движение резьбы винта будет направлено вдоль тока то вращательное движение головки укажет направление силовых линий магнитного поля.

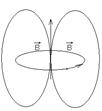
Для определения направления силовых линий магнитного поля созданного кольцевым проводником с током так же удобно использовать правило правого винта. Согласно которому если головку винта с правой нарезкой вращать по направлению тока то поступательное движение резьбы винта укажет направление силовых линий магнитного поля. Силовые линии магнитного поля являются замкнутыми. Если силовые линии ЭСП начинаются на плюсе и заканчиваются на минусе то силовые линии МП замыкаются сами на себя.

Для создания и концентрации МП в некоторой ограниченной области пространства применяют устройства называемые соленоидами.

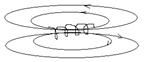Это проводник который наматывается на цилиндрический каркас и при прохождении тока по данному проводнику МП концентрируется непосредственно в нутрии данного соленоида. Для определения направления МП созданного соленоидом удобно использовать правило правой руки: Если правой рукой охватить соленоид так что четыре пальца будут направлены вдоль тока то отогнутый на 90 градусов большой палей укажет направление силовых линий МП.

Замкнутость силовых линий МП косвенно говорит об отсутствии свободных магнитных зарядов на которых могли бы начинаться силовые линии МП. Опытный факт об отсутствии свободных магнитных зарядов был обобщён Максвеллом и вошёл в систему уравнений Максвелла.

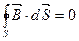
В дифференциальной форме

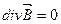
Данное уравнение – теорема Гаусса для МП и уравнение обобщающее закон кулона для МП. Данное уравнение описывает фундаментальный физический закон. Исходя изданного закона а так же закона обобщающего опытный факт о природе вихрей МП (о природе вихревого МП) можно получит закон Био-Саварра с помощью которого удобно рассчитывать МП созданное проводниками с током имеющих сложную конфигурацию. Для вывода закона Био-Саварра введём вспомогательную векторную функцию (Векторный потенциал) МП. Эта функция не имеет физического смысла а является вспомогательной применяемой для вывода выше названного закона.

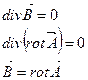
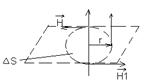
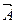- векторный потенциал МП. В отличии от скалярного потенциала ЭСП эта функция лишена физического смысла. Запишем уравнение обобщающее опытный факт о природе вихрей МП. Этот опытный факт можно обнаружить следующим образом. Если проводник с током протыкает некоторую диэлектрическую пластину на которой беспорядочно насыпаны металлические опилки то при пропускании тока по данному линейному проводнику опилки начинают выстраиваться по концентрическим окружностям центр которой лежит на данном проводнике. Это говорит о том что опилки испытывают силовое воздействие со стоны магнитного поля созданного данным проводником с током.

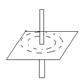Анализ данного эксперимента показывает что между напряжённостью МП и током протекающим по данному проводнику существует следующая взаимосвязь.

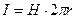
r – расстояние от проводника с током I до точки наблюдения (точки в которой необходимо определить напряжённость H); Н – напряжённость МП.

Более общая запись данного уравнения для проводника более сложной конфигурации:

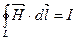
Применим к последнему уравнению тождество векторного анализа формулу Стокса. Получим данное уравнение в дифференциальной форме.

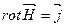
- плотность тока.

Предполагаем что поверхность замкнутая данным контуром 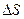. Устремим 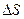к нулю.

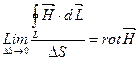
С другой стороны 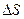можно трактовать как площадь поперечного сечения линейного проводника с током.

Исходя из полученного уравнения обобщён опытный факт об отсутствии свободного магнитного заряда и из уравнения обобщающего опытный факт о природе вихрей МП получим закон Био-Саварра.

Учитывая введённые выше понятия векторного потенциала

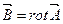
Так как 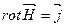, то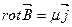

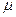- абсолютная магнитная проницаемость среды.

Заменим 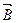на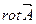

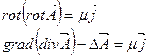
На векторный потенциал А накладываем дополнительные условия, а именно, что

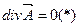
С учётом выше изложенного (*) преобразуем

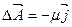
Полученное уравнение называется уравнением потенциала для векторного потенциала МП оно по форме совпадает с аналогичным дифференциальным уравнением для скалярного потенциала

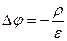
Решение данного уравнения можно записать подобно решению уравнения Пуассона для скалярного потенциала ЭПС

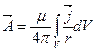
r – расстояние от элементарного объема dV по которому протекает ток плотностью 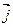до точки наблюдения в которой определяем векторный потенциал МП А. Из представленного выражения следует что направление векторного потенциала определяется направлением тока созданного МП с данным векторным потенциалом.

Рассмотрим линейный ток. Линейным называется такой ток плотность которого будет постоянна в поперечных сечениях проводника в этом случае величину плотности тока

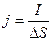
Саму величину вектора j мы можем определить

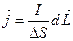
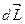- элементарная длинна элемента данного проводника по которому протекает ток I имеющий плотность 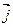. Направление 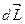совпадает с направлением тока протекающего по данному проводнику.

Тогда величину 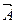можно записать

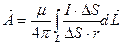
L – длинна проводника

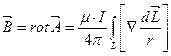
МП так же как и поле электрическое подчиняется принципу суперпозиции согласно которому для вычисления основных силовых характеристик МП (индукции и напряжённости) созданными проводником с током сложной конфигурации длинны L. Необходимо данный проводник разбить на элементарные проводники длинной 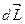. Найти в искомой точке пространства индукцию МП созданную каждым элементарным проводником, а индукцию результирующего МП определяют как геометрическую сумму элементарных индукций 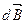созданных каждым элементарным проводником с током длинной 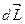. Поэтому величину стоящую под интегралом умножаемую на коэффициент фигурирующий перед интегралом можно трактовать как индукцию МП созданную элементарным отрезком.

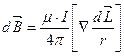
Раскроем векторное произведение которое фигурирует в под интегральном выражении

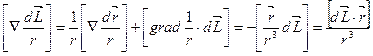
Отсюда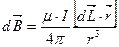

Полученное выражение является законом Био-Саварра. С помощью него можно определить как модуль так и направление вектора магнитной индукции МП созданного элементарным отрезком длинной 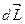с током I на расстоянии r от данного отрезка.

Для определения индукции МП созданного проводником сложной формы применяем принцип суперпозиции. При применении этого принципа необходимо произвести суммирование которое сводится к интегрированию.

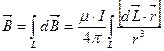
Дата добавления: 2013-12-12