
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Простейшие приемы экономико-математического анализа
|
|
|
|
1. Метод расширения факторной системы, когда числитель и знаменатель кратной модели умножается на один и тот же показатель. В результате получают мультипликативную модель состоящую из новых факторов:
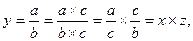
где 
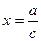 ,
, 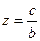 .
.
Пример
ПТ=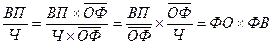 .
.
2. Метод сокращения факторной системы, когда числитель и знаменатель кратной модели делят на один и тот же показатель, что приводит к получению кратной модели, состоящей из новых факторов:
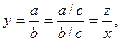
z=a/c, x=b/c.
Пример
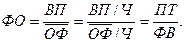
3. Метод удлинения факторной системы, когда числитель кратной модели представляют в виде суммы факторов и получают вместо кратной модели аддитивную:
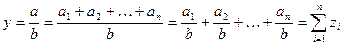 ,
,
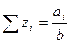 .
.
К экономико-математическим методам также относят интегральный метод. При его использовании последовательность подстановок значения не имеет. Этот метод основан на расчете влияния факторов с помощью математических формул, причем для каждого конкретного случая и вида факторной системы расчетные формулы строго индивидуальны. Интегральный метод может заменить индексный метод, метод цепных подстановок, «разниц».
| Вид факторной системы | Расчетная формула |
| 1. Мультипликативная двухфакторная система типа y=a*b | 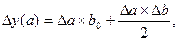
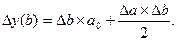
|
| 2. Кратная двухфакторная система типа y=a/b | 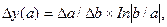
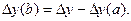
|
| 3. Мультипликативная трехфакторная система типа y=a*b*с | 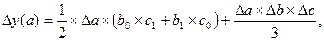
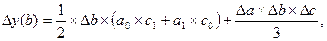
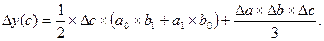
|
Экономические процессы и явления носят сложный характер и не всегда могут быть измерены непосредственно, так как находятся под влиянием целого ряда факторов, не поддающихся количественной оценке. В этом случае в экономическом анализе применяются приемы стохастического анализа.
Среди методов стохастического анализа наиболее широко известны корреляционный, регрессионный, спектральный, дисперсионный анализ и группировки.
Регрессионный анализ широко используется в целях прогнозирования значений анализируемого показателя. Из большого числа функций для решения экономических задач чаще всего используют линейную функцию вида y=a+b*x, а из нелинейных y=a+b/x.
Для решения уравнения прямой рассчитываются параметры a и b на основании решения системы уравнений:
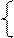
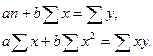
Для того, чтобы в экономических расчетах можно было использовать данные уравнения, необходимо убедиться, что связь между показателями x и y действительно существует. Для этого рассчитывается коэффициент корреляции:
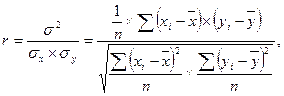
где xi, yi – значения анализируемых показателей,
n – количество наблюдений.
Критерии оценки линейной связи между показателями на основе коэффициента корреляции
| Величина коэффициента корреляции | Характер связи |
До 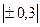
| Практически отсутствует |
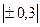 - -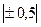
| Слабая |
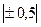 - -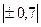
| Умеренная |
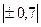 - -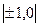
| Сильная |
Для удобства расчетов целесообразно использовать таблицу следующей формы:
| xi | yi | (xi-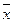 ) )
| (xi-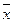 ) )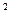
| (yi-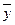 ) )
| (yi-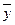 ) )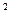
| (xi-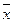 )(yi- )(yi-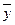 ) )
| x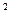
| xy |
| А | ||||||||
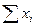
| 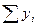
| 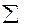 (xi- (xi-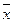 ) )
| 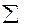 (xi- (xi-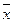 ) )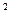
| 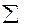 (yi- (yi-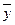 ) )
| 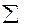 (yi- (yi-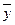 ) )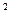
| 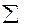 (xi- (xi-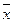 )(yi- )(yi-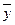 ) )
| 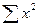
| 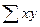
|
|
|
|
|
Дата добавления: 2013-12-12; Просмотров: 223; Нарушение авторских прав?; Мы поможем в написании вашей работы!