Макроэкономические модели

Рассмотрите экономику с двумя группами потребителей. Потребители первой группы потребляют в соответствии с кейнсианской функцией потребления: c_1t=by_1t, где y_1t – доход потребителей 1-ой группы в период t, а b – предельная склонность к потреблению (0<b<1). Будем считать, что доход потребителей 1-ой группы составляет λ в общем доходе: y_1t=λy_t. Потребители второй группы выбирают потребление в соответствии с теорией перманентного дохода из решения задачи максимизации ожидаемой полезности:

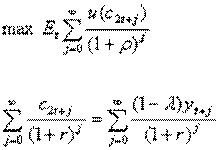
где ρ – дисконт времени, E_t- ожидания, сформированные в момент t.

А) Полагая, что ρ=r и функция полезности квадратичная

,

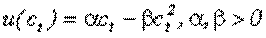найдите оптимальное потребление для второй группы.

Б) Пусть динамика совокупного дохода задана как ,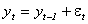

где ε_t –ошибка, причем Eε_t=0 и ошибки независимы.

Пусть совокупное потребление равно: c_t=c_t1+c_t2. Каково соотношение между дисперсией Δc_t и дисперсией Δy_t?

В) Предположим, что в реальности мы наблюдаем, что дисперсия Δc_t меньше, чем дисперсия Δy_t. Принимая во внимание вывод о соотношении этих дисперсий, полученный в пункте (б), может ли мы из этого эмпирического наблюдения сделать вывод, что большинство людей ведет себя в соответствии с теорией перманентного дохода, то есть λ=0?

Г) Полагая, дисперсия Δc_t меньше, чем дисперсия Δy_t, какой вывод мы можем сделать относительно влияния временного снижения налогов на совокупное потребление?

Решение

а) Обозначим множитель Лагранжа, соответствующий бюджетному ограничению через μ и выпишем условия первого порядка для задачи максимизации ожидаемой полезности:

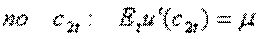
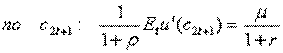
Поделив эти условия, получим:

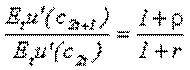
Полагая, что ρ=r, получим:

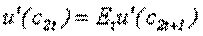
В силу квадратичности функции полезности имеем:

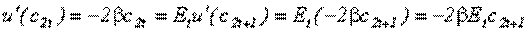
откуда получаем

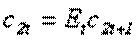
Подставляем в бюджетное ограничение

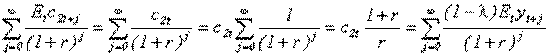
откуда находим потребление второй группы в период t:

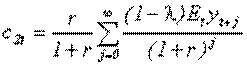
Итак, потребители второй группы в каждый период будут потреблять фиксированную долю r/(1+r) своего жизненного дохода.

Б) Поскольку y_t = y_t-1+ε_t, причем

,

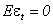то

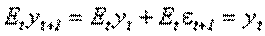
и по аналогии можно показать, что

.

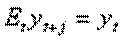Найдем изменение потребления для каждой группы.

;

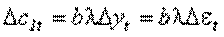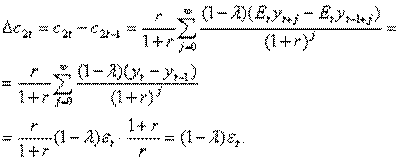
Итак, изменение совокупного потребления равно:

.

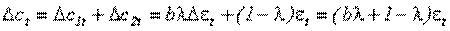Найдем дисперсию изменения потребления:

,

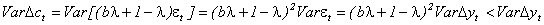поскольку b<1 и мы предполагали, что λ>0.

В) Если мы наблюдаем, что

,

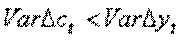то это означает, что λ>0. Действительно, если бы λ=0, то согласно рассмотренной модели

,

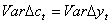но это противоречит нашим наблюдениям, следовательно λ>0, то есть в рассматриваемой экономике мы имеем, как потребителей, испытывающих ограничение ликвидности и потому имеющих кейнсианскую функцию потребления, так и тех, кто ведет себя согласно теории перманентного дохода.

Г) Рассмотрим временное снижение паушального налога на величину ΔT. Для потребителей первой группы имеем:

.

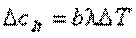Для потребителей второй группы:

,

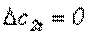однако, совокупное потребление все же изменится:
.

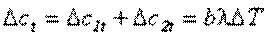Дата добавления: 2013-12-12