Формула Симпсона

Формула трапеций

Рассмотрим интервал [0, h ], h > 0

Предположим, что f (x) Î C ²[0, h ]. Соотношение (7) запишем в виде:

, (12)

где взяты два узла x₀ = 0, x₁ = h и соответствующие веса q ₀ = q ₁ = h /2.

Получаемая квадратурная формула

, (13)

называется формулой трапеций для одного шага. Название связано с тем, что (13) при положительных значениях f (0), f (h) является площадью трапеции с основаниями f (0), f (h) и высотой h.

Доказано, что погрешность для (12)

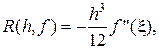(14)

где x – некоторая точка интервала [ 0, h ]. Заметим, что (13) так же, как формула прямоугольников точна для полиномов первой степени.

Рассмотрим интервал [ –h, h ], h > 0. Предположим, что f (x) Î C ⁴[– h, h ].

Для соотношения (7) возьмем три узла x₀ = x_{i –1} = – h, x₁ = x_i =0, x₂ = x_{i +1}= h. Соответствующие им весовые коэффициенты получим из аппроксимации f (x) параболой, построенной на точках (– h, f (– h)), (0, f (0)), (h, f (h)) в виде квадратного многочлена y = ax ² + bx + c. Для получения коэффициентов a, b и c построим многочлен Лагранжа второй степени, проходящий через выбранные точки:

.

Вычисляем интеграл:

(16)

Тогда соотношение (7) запишется в виде:

(17)

и называется формулой Симпсона (парабол).

Доказано, что погрешность для формулы Симпсона оценивается соотношением:

, (18)

где xÎ [– h, h ].

Из соотношения (18) следует, что квадратурная формула Симпсона точна для полиномов третьей степени.

Отметим, что при применении простейших квадратурных формул требуются вычисления значения подынтегральных функций f (x):

а) в одной точке – для формулы прямоугольников;

б) в двух точках – для формулы трапеций;

в) в трех точках – для формулы Симпсона.

Однако, несмотря на малый объем вычислений, область практических применений простейших квадратурных формул ограничена лишь малыми интервалами, поскольку при увеличении h погрешность становится значительной, как видно из формул для погрешностей, что и выдвигает необходимость использования т.н. составных квадратурных формул.

Дата добавления: 2013-12-11