Метод Лагранжа-Эйлера

Лекция 7

Потенциальная энергия манипулятора

Обозначим полную потенциальную энергию манипулятора через Р, а потенциальную энергию i -го звена – через 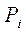. Тогда:

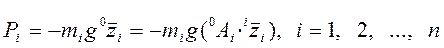. (6-8)

Суммируя потенциальные энергии всех звеньев, получаем:

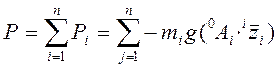. (6-9)

Здесь 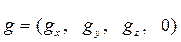- вектор-строка, описывающая гравитационное ускорение в базовой системе координат. В земной системе координат 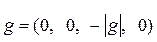, а g – ускорение свободного падения на поверхности Земли (g =9,8062 м/с²).

Полное описание движения манипулятора можно получить, применяя метод Лагранжа-Эйлера для неконсервативных систем. Описав кинематику манипулятора с помощью матричного представления Денавита-Хартенберга, можно получить уравнение динамики. Такое совместное использование Д-Х-представления и метода Лагранжа приводит к компактной векторно-математической форме уравнений движения, удобной для аналитического исследования и допускающей реализацию на ЭВМ.

Вывод уравнений динамики движения манипулятора основан на следующем:

1. На описании взаимного пространственного расположения систем координат i -го и (i -1)-го звеньев с помощью матрицы преобразования однородных координат 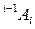. Эта матрица преобразует координаты произвольной точки относительно i -й системы координаты этой же точки относительно (i -1)-й системы координат.

2. На использовании уравнения Лагранжа-Эйлера:

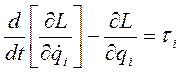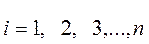; , (7-1)

где L -функция Лагранжа (L = K-P);

K -полная кинетическая энергии манипулятора;

P -полная потенциальна энергия манипулятора

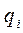-обобщённые координаты манипулятора;

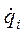- первая производная по времени обобщённых координат;

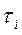-обобщённые силы (или моменты), создаваемые в i -м сочленении для реализации заданного движения i -го звена.

Для того, чтобы воспользоваться уравнением Лагранжа-Эйлера, необходимо выбрать систему обобщённых координат. Обобщённые координаты представляют собой набор координат, обеспечивающий, полное описание положения рассматриваемой физической системы в абсолютной системе координат. Существуют различные системы обобщенных координат, пригодные для описания простого манипулятора с вращательными и поступательными сочленениями. Однако, поскольку углы поворотов в сочленениях непосредственно доступны измерению с помощью потенциометров или других датчиков, то они составляют наиболее естественную систему обобщенных координат. В этом случае обобщённые координаты совпадают с присоединенными переменными манипулятора. В частности, если i -е сочленение вращательное, то 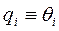, если же i -е сочленение поступательное, то .

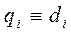Запишем выражение для функции Лагранжа:

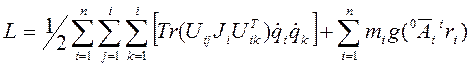. (7-2) Здесь вместо скалярного произведения используется оператор 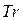(след матрицы ).

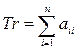Подставив это выражение в уравнение Лагранжа, получим выражение для обобщённой силы 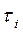, которую должен развить силовой привод i -го сочленения, чтобы реализовать задание движение i -го звена манипулятора:

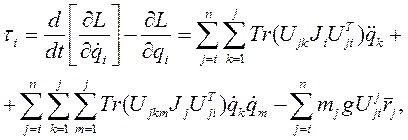(7-3)

.

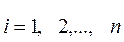Выражение (10-11) можно представить в более простой форме:

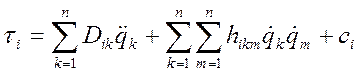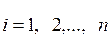, , (7-4)

или в матричном виде:

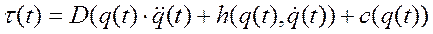, (7-5)

где 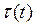- вектор (размерностью n ×1) обобщённых сил, создаваемых силовыми приводами в сочленениях манипулятора:

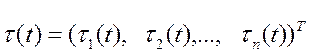; (7-6)

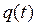- вектор (размерностью n ×1) присоединенных переменных манипулятора:

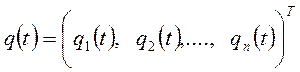; (7-7)

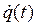- вектор (размерностью n ×1) обобщённых скоростей:

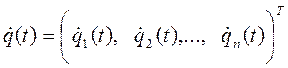; (7-8)

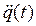- вектор (размерностью n ×1) обобщённых ускорений:

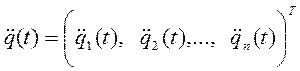; (7-9)

D(q) – симметричная матрица размерностью n × n, элементы которой даются выражением:

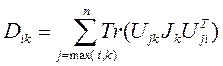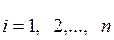, ; (7-10)

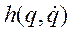- вектор (размерностью n ×1) кориолисовых и центробежных сил:

,

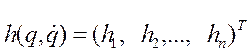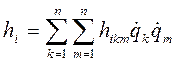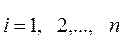, , (7-11)

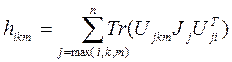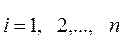, ; (7-12)

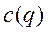- вектор (размерностью n ×1) гравитационных сил:

,

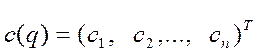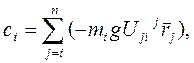
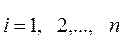. (7-13)

Коэффициенты 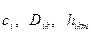в выражениях (7-10) – (7-13) являются функциями как присоединенных переменных, так и динамических параметров манипулятора. Их называют динамическими коэффициентами манипулятора. Физический смысл динамических коэффициентов легко понять из уравнений (7-10) – (7-13), описывающих динамику движения манипулятора.

1. Коэффициенты 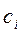, определяемые равенством (7-13), учитывают силу тяжести, действующую на каждое из звеньев манипулятора.

2. Коэффициенты 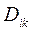, определяемые равенством (7-10), устанавливают связь действующих в сочленениях сил и моментов с ускорением присоединенных переменных. В частности, при i = k коэффициент 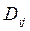связывает момент 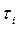, действующий в i -м сочленении, с ускорением i -й присоединенный переменной. Если 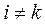, то 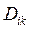определяет момент (или силу), возникающий в i -м сочленении под действием ускорения в k -м сочленении. Поскольку матрица инерции симметрична и 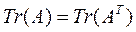то .

3. Коэффициенты 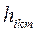, определяемые равенствами (7-11) и (7-12), устанавливают связь действующих в сочленениях сил и моментов со скоростями изменения присоединенных переменных. Коэффициент 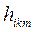определяет связь момента, возникающего в i -м сочленении в результате движения в k -м и m -м сочленениях, со скоростями изменения k -й и m -й присоединенных переменных. В соответствии с физическим смыслом .

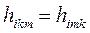При вычислении рассмотренных коэффициентов полезно знать, что некоторые из этих коэффициентов могут иметь нулевые значения по одной из следующих причин:

1. Конкретная кинематическая схема манипулятора может исключить динамическое взаимовлияние движений в некоторых парах сочленений (коэффициенты).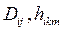

2. Некоторые из коэффициентов 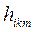присутствуют в формулах (5-20) и (7-11) чисто фиктивно, будучи нулевыми в соответствии с физическим смыслом. Например, коэффициент 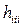всегда равен нулю, так как центробежная сила, порожденная движением в i -м сочленении, на само i -е сочленение влияния не оказывает, хотя и влияет на другие сочленения, т.е. 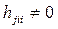при .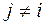

Некоторые из динамических коэффициентов могут принимать нулевые значения в отдельные моменты времени при реализации определённых конфигураций манипулятора

Дата добавления: 2013-12-12