Формула Симпсона. Обозначим значение функции f(х) в точках xi : fi = f(хi), i =

Формула трапеций

Обозначим значение функции f (х) в точках x_i: f_i = f (х_i), i = .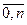

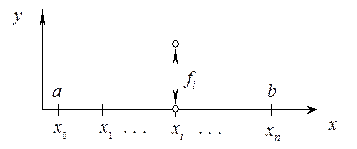
Тогда по аналогии с формулой для прямоугольников из (12) получим составную квадратурную формулу трапеций.

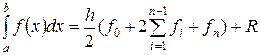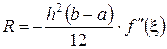; . (21)

Здесь xÎ [ a, b ].

Разобьем интервал [ a, b ] на четное число частичных интервалов 2 m, где 2 m = (b – a)/ h.

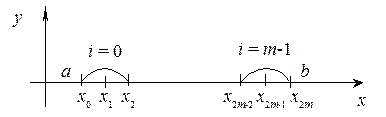
Суммируя (17)

;

получим формулу Симпсона

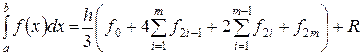; (22)

где 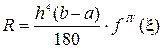, x Î [ a, b ].

Заметим, что в отличие от простейших формул при оценке их погрешности в составных формулах (20), (21) и (22) нахождение точки x Î [ a, b ] однозначно неопределенно.

На конкретном примере можно оценить точный выбор точки x для рассчитанных выше составных формул для интервала [ a, b ].

Пример. Вычислить интеграл 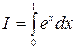с помощью трех квадратурных формул и сравнить ответ с точным значением I = e – 1 = 1,7182818.

Возьмем произвольно h = 0,1. Тогда

=

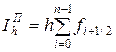= 0,1(e ^0,05+ e ^0,15+ e ^0,25+ e ^0,35+ e ^0,45+ e ^0,55+ e ^0,65+ e ^0,75+ e ^0,85+ e ^0,95) = 1,7176;

=

= 0,05[ e ^0,0 +2(e ^0,1+ e ^0,2+ e ^0,3+ e ^0,4+ e ^0,5+ e ^0,6+ e ^0,7+ e ^0,8+ e ^0,9) + e ¹] = 1,7197;

=

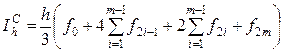= 0,1/3×[ e ^0,0 +4(e ^0,1+ e ^0,3+ e ^0,5+ e ^0,7+ e ^0,9) +2(e ^0,2+ e ^0,4+ e ^0,6+ e ^0,8) + e ¹] = 1,7182828.

Точное значение I позволяет определить точки x для формул соответствующих погрешностям R в (20), (21), (22).

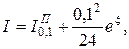x = 0,365;

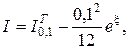x = 0,532;

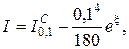x = 0,588.

Следовательно, для каждой квадратурной формулы следует выбирать свое x с точки зрения оценки точности, что связано с очевидными расчетными трудностями. Утверждение, что повышение точности вычисления интеграла напрямую связано с уменьшением шага h также не совсем верно.

Из практики известно, что, начиная с некоторого (n ₀) погрешность вычислений снова начинает увеличиваться по причине округлений малых величин, т.е.

В общем случае погрешность интегрирования может быть представлена в виде:

,

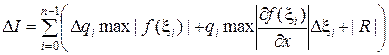где D q_i – абсолютная погрешность весов, Dx _i – абсолютная погрешность узлов, R – погрешность квадратурной формулы.

В связи с вышеизложенным, при вычислении интеграла для выбранной формулы численного интегрирования по заданной точности e, выбор шага h производится из следующих соображений:

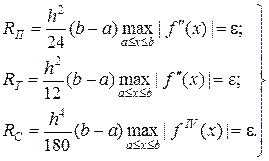(23)

Соотношение (23) означает, что шаг h, а, следовательно, и число точек n, в которых вычисляется f (x), определяется значением x с наихудшим поведением f (x) с точки зрения погрешности R.

Однако такое правило разбиения интервала интегрирования может приводить к избыточным вычислениям, если f (x) имеет только частные интервалы с ее «плохим» поведением относительно длины отрезка [ a, b ].

Для примера рассмотрим подынтегральную функцию типа: f (x) = e ^{– x /s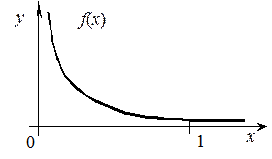} на отрезке [0, 1] с шагом h =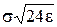. Очевидно, что шаг очень мал согласно (23) для обеспечения заданной точности для всего отрезка [0,1], т.е. возникает потребность для устранения избыточных вычислений разбивать интервал [ a, b ] на частичные интервалы различной длины, которая определяется свойствами f (x) и заданной точностью интегрирования.

Таким образом, возникает задача применения простейших квадратурных формул интегрирования с переменным шагом интегрирования на отрезке [ a, b ]. Данная ситуация будет рассмотрена ниже.

Дата добавления: 2013-12-11