Линейные деформации прямо пропорциональны нормальным напряжениям

Рис. 8.1.

Рис. 7.1.

Рис. 6.2.

Рис. 6.1.

Рис. 5.2.

Рис. 5.1.

Рис. 4.1.

Е допущение, или принцип Сен-Венана. В точках тела, достаточно удаленных от мест приложения нагрузок, внутренние силы весьма мало зависят от конкретного способа приложения этих нагрузок.

Е допущение, или принцип независимости действия сил. Результат воздейст­вия на тело системы сил равен сумме резуль­татов воздействия тех же сил, прилагае­мых к телу последова­тельно и в любом порядке.

Е допущение. Материал конструкции изотропен, т. е. обладает во всех направ­лениях одинаковыми свойствами.

Исследования показывают, что кристаллы, из которых состо­ят многие материалы, обладают в различных направлениях весь­ма различными свойствами.

Однако у материалов, имеющих мелкозернистую структуру, благодаря большому количеству кристаллов, расположенных в беспорядке, свойства в разных направлениях выравниваются, «осредняются», и можно считать эти материалы практически изотроп­ными.

Для таких материалов, как дерево, железобетон, пластмас­сы, указанное допущение выполняется лишь приблизительно.

Материалы, свойства которых в разных направлениях раз­личны, называются анизо­тропными.

4-е допущение. В теле до приложения нагрузки нет внутрен­них (начальных) уси­лий. Изменению формы и размеров тела под нагрузкой сопротивляются силы взаимодей­ствия между части­цами материала, называемые силами упругости. В дальнейшем, говоря о внутренних силах, будем иметь в виду именно эти силы упругости, не принимая во вни­мание молекулярные силы, имею­щиеся и в ненагруженном теле.

Это допущение полностью не выполняется ни для одного материала. В стальных де­талях имеются внутренние силы, вы­званные неравномерностью остывания, в дереве – не­равномер­ностью высыхания, в бетоне – в процессе твердения.

Значение этих сил конструктору обычно неизвестно. В тех случаях, когда есть осно­вания предполагать, что эти силы значительны, стараются определить их эксперименталь­ным путем.

Под словами «результат воздействия» в зависимости от конкретной задачи следует понимать деформации, внутренние силы, возникающие в теле, и пере­мещения отдельных точек.

Необходимо иметь в виду, что действие отдельных сил системы должно рассматри­ваться вместе с соответствующими им реакциями связей.

Принцип независимости дейст­вия сил, широко применяемый в теоретической меха­нике для абсолютно твердых тел, к деформируемым телам применим лишь при следую­щих двух условиях:

1. Перемещения точек приложения сил малы по сравнению с размерами тела.

2. Перемещения, являющиеся результатом деформации тела, линейно зависят от дей­ствующих сил. Такие, тела (системы) называют линейно деформируемыми или подчи­няющимися зако­ну Гука.

В обычных конструкциях оба эти условия выполняются, и поэтому принцип незави­симости действия сил при силовом расчете конструкций используется широко.

Этот принцип во многих случаях позволяет производить замену одной системы сил другой системой, статически эквива­лентной, что может упростить расчет.

Тема №3. Понятие о реальном объекте и расчетной схеме.

Каждое сооружение состоит из множества различных элементов и деталей, в строительстве которые принято делить на два основных вида: несущие и ограждающие. К несущим относятся элементы, которые воспринимают и передают на землю нагрузки от веса конструкции, веса технологического или какого-либо другого оборудования, а также от климатических воздействий (веса снега, действия температуры и т. п.).

Ограждающие элементы, например две­ри, окна, перегородки, навесные панели в каркасных зданиях и т.п., как правило, не принимают участия в передаче нагрузки на землю; они воспринимают только собственный вес, а также временные нагрузки, например от ветра, действующего в пределах площади соответствующего элемента. Поэтому при расчетах сооружений на прочность и жесткость принимается, что вес ограждающих конструкций передается на несущую конструкцию, схематическое изображение которой называется расчетной схемой. Проектировщик производит расчет системы, состоящей только из несущих элементов, указанных в расчетной схеме.

Различают несколько основных видов несущих элементов, входящих в расчетную схему:

1) стержни, длина которых значи­тельно превышает два других размера (рис. 1.1, а)

Ось бруса – это линия, последовательно соединяющая центры тяжести его поперечных сечений. Плоская фигура, имеющая свой центр тяжести на оси и нормальная к ней, называется его поперечным сечением;

2) пластины, у которых один размер d (толщина) значительно меньше двух других размеров а и b (рис. 1.1,б);

3) оболочки, которые отличаются от пластин тем, что они очерчены по криволинейной поверхности (рис. 1.1, в, г);

4) объемные тела, у которых все три генеральных размера примерно одного порядка, например блоки фундаментов, опоры мостов и т.п. (рис. 1.1, д).

Рис. 3.1.

При составлении расчетных схем необ­ходимо учитывать способы соединения между собой элементов конструкции. Места соединения элементов называются узлами (в расчетном виде, для элементов, передающих нагрузку – опорами), которые могут отличаться различными конструктивными решениями.

Опоры, рассматриваемых как плоские системы, быва­ют трех основных типов.

1. Шарнирно-подвижная опора. Такая опора не препятствует враще­нию конца балки и его перемещению вдоль плоскости качения. В ней может возникать только одна реакция, которая перпендикулярна плоскости качения и прохо­дит через центр катка.

Подвижные опоры дают возможность балке беспрепятствен­но изменять свою длину при изменении температуры и тем самым устраняют возможность появления температур­ных на­пряжений.

2. Шарнирно-подвижная опора. Такая опора допускает вращение конца балки, но устраняет поступа­тельное перемещение ее в любом направле­нии. Возникающую в ней реакцию можно разложить на две составляющие – гори­зон­тальную и вертикальную.

3. Жесткая заделка, или защемление. Такое закрепление не допус­кает ни линейных, ни угловых перемещений опорного сечения. В этой опоре может в об­щем случае возникать реакция, которую обычно раскладывают на две составляющие (вер­тикальную и горизонтальную) и момент защемления (ре­активный момент).

Тема №3а. ВНЕШНИЕ СИЛЫ (НАГРУЗКИ)

Нагрузки, действующие на сооружения и их элементы, пред­ставляют собой силы или пары сил (моменты), которые мо­гут рассматриваться как сосредоточенные или распре­делен­ные.

Правда, в природе сосредоточенных сил не бывает. Все реальные силы – это силы, распределенные по некоторой площа­ди или объему.

Сосредоточенные нагрузки выражаются в ньютонах, кило-ньютонах или меганьюто­нах (Н, кН, МН).

Распределенные нагрузки могут быть поверхностными (на­пример, давление ветра или воды на стенку) и объемными (на­пример, сила тяжести тела, силы инерции).

Силу тяжести стержня, учитывая небольшие размеры его поперечного сечения по сравнению с длиной, рассматривают обычно не как объемную нагрузку, а как нагрузку, распределен­ную по длине стержня.

Распределенные нагрузки выражаются в единицах силы, отнесенных к единице длины, или к единице поверхности, или к единице объема. И сосредоточенные, и распре­деленные нагрузки могут быть как статическими, так и динамиче­скими.

Статическими называются нагрузки, которые изменяют свою величину или точку приложения (или направление) с очень небольшой скоростью, так что возникающими при этом ускоре­ниями можно пренебречь. При действии таких нагрузок колеба­ния сооруже­ний и их частей пренебрежимо малы.

Динамическими называются нагрузки, изменяющиеся во времени с большой скоро­стью (например, ударные нагрузки). Действие таких нагрузок сопровождается возникно­вением коле­баний сооружений. При колебании же вследствие изменения скорости колеб­лющихся масс возникают силы инерции, пропор­циональные (по второму закону Ньютона) колеблющимся мас­сам и ускорениям. Эти силы инерции могут во много раз превос­ходить те же нагрузки, приложенные статически.

При расчете строительных сооружений величины расчетных нагрузок регламенти­руются техническими условиями и нормами проектирования.

Тема №4. ДЕФОРМАЦИИ И ПЕРЕМЕЩЕНИЯ

Как было отмечено ранее, все тела под действием приложенных к ним внешних сил в той или иной степени деформируются, т. е. изменяют свои размеры или форму либо и то и другое одновременно.

Изменение линейных размеров тела или его частей называется л инейной, а измене­ние угловых размеров – угловой деформациями. При этом увеличение размеров тела на­зывается удлинением, а уменьшение размеров – укорочением.

Если деформации изменя­ются по объему тела, то говорят о деформации в данной точке тела, в определенном направлении.

Если на поверхности тела, вблизи исследуемой точки, нанести весьма малый прямо­угольник 1234 (рис. а), то в результате деформации этот прямоугольник в общем случае примет вид параллелограмма 1' 2' 3' 4' (рис. 4.1).

Длины сторон прямоугольника изменятся (увеличатся или уменьшатся), а стороны повернутся по отношению к первоначальному положению.

Если, например, длина стороны 23 изменится на величину Ds, то отношение:

называется средней линейной деформацией (в данном случае средним удлинением) в точке 2.

При уменьшении отрезка S в пределе получим:

– где величина e называется истинной линейной деформацией в точке 2 внаправ­лении 23.

Изменение первоначального прямого угла между сторонами рассматриваемого пря­моугольника g = a + b будет характеризовать угловую деформацию (или угол сдвига) в данной точке.

Опыт показывает, что деформации, как линейные, так и угловые, могут после снятия нагрузки или полностью исчезнуть, или исчезнуть лишь частично (в зависимости от мате­риала и величи­ны нагружения).

Деформации, исчезающие после разгрузки тела, называются упругими, а свойство тел принимать после разгрузки свою первоначальную форму называется упругостью.

Деформации же, сохраняемые телом и после удаления нагрузки, называются оста­точными или пластическими, а свойство материалов давать остаточные деформации на­зывается пластичностью.

Зная деформации тела во всех его точках и условия закрепления, можно определить перемещения всех точек тела, т. е. указать их положение (новые координаты) после де­формации. Для нормальной эксплуатации сооружения деформации его отдельных элемен­тов должны быть, как правило, упругими, а вызванные ими перемещения не должны пре­восходить по величине определенных допускаемых значений. Эти условия, выраженные в форме тех или иных уравнений, называются условиями жесткости. В некоторых случаях допускаются небольшие пластические деформации (для конструкций из железобетона, пластмасс и для конструкций из металла при действии высоких температур).

Тема №5. МЕТОД СЕЧЕНИЙ

Внутренние силы (силы упругости), возникающие в теле под действием нагрузки,– силы непрерывно распределенные (в со­ответствии с принятым допущением о непре­рывности материала тела).

Как определяются эти силы в любой точке тела, будет пока­зано ниже.

Теперь же займемся определением тех равнодействующих усилий (в том числе и моментов), к которым приводятся в сече­нии эти силы упругости. Эти равнодействующие усилия пред­ставляют собой не что иное, как составляющие главного вектора и главного момента внутренних сил.

Для определения внутренних усилий (или внутренних сило­вых факторов) применя­ется метод сечений, заключающийся в следующем.

Для тела, находящегося в равновесии (рис. 5.1), в интересу­ющем нас месте мысленно делается разрез, например по а – а. Затем одна из частей отбрасывается (обычно та, к ко­торой приложено больше сил).

Взаимодействие частей друг на друга заменяется внутренними усилиями, которые уравновешивают внешние силы, действующие на отсеченную часть. Если внешние силы лежат в одной плоскости, то для их уравновешивания необходимо в общем случае прило­жить в сечении три внутрен­них усилия:

– силу N, направленную вдоль оси стержня и называе­мую продольной силой;

– силу Q, действующую в плоскости попе­речного сечения и называемую попереч­ной силой;

– момент М, плоскость действия которого перпендикулярна плоскости сечения. Этот момент возникает при изгибе стержня и называется из­гибающим моментом.

После этого составляют урав­нения равновесия для отсечен­ной части тела, из кото­рых и оп­ределяются N, Q, M. Действи­тельно, проецируя силы, дейст­вующие на отсечен­ную часть, на направление оси стержня и при­равнивая сумму проекций нулю, найдем N; проецируя силы на направление, перпендикулярное оси стержня, определим Q; приравни­вая нулю сумму моментов относительно какой-либо точки, определим М.

Итак, для нахождения внутренних усилий необходимо:

1) разрезать стержень или систему стержней;

2) отбросить одну часть;

3) приложить в сечении усилия, способные уравновесить внешние силы, действующие на отсеченную часть;

4) найти значения усилий из уравнений равновесия, составленных для отсеченной части.

В частном случае в поперечном сечении стержня могут возникать:

1. Только продольная сила N. Этот случай нагружения называется растяжением (если сила N направлена от сечения) или сжатием (если продольная сила направлена к сечению).

2. Только поперечная сила Q. Это случай сдвига.

3. Только крутящий момент М_к. Это случай кручения.

4. Только изгибающий момент М_х или M_y. Это случай изгиба.

5. Несколько усилий, например изгибающий и крутящий моменты. Это случаи слож­ных деформаций (сложное со­противление), которые будут рассмотрены позже.

Если число неизвестных усилий равно числу уравнений равновесия (уравнения статики åх=0; åy=0; åМ=0;), задача называется статически определимой, если же число неизвестных усилий больше числа уравнений равновесия – статически неопределимой.

Для статически неопределимых задач кроме уравнений равновесия необходимо использовать еще дополнительные уравне­ния при рассмотрении деформации системы.

Рассмотрим на примере применение метода сечений.

Пример. Определить усилия в стержнях АВ и ВС системы, изображенной на рис.5.2.

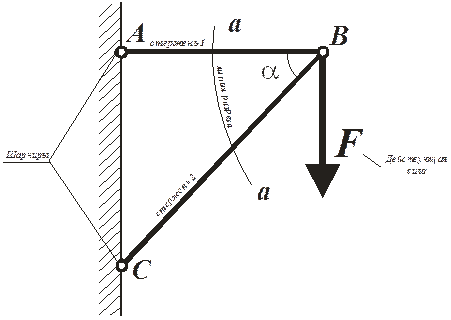
Решение. Для определения усилий в стержнях АВ и ВС применим метод сечений. Проведем сечение а – а по стержням, отбросим левую часть и рассмотрим равновесие правой части.

Усилия в обоих стержнях вначале предположим растягивающими (растягивающие усилия на чертеже направлены от узла) и обозначим их N₁ и N₂. Составим уравнения равновесия отсеченной части системы:

– P – N×sina = 0. Отсюда N₂ = –

Знак минус указывает, что усилие N₂ будет не растягивающим, как мы предположили, а сжимающим. Составим второе уравнение равновесия:

– N – N×cosa = 0.

Подставив значение N ₂= – , получим N₁ = P∙ctga.

Тема №6. НАПРЯЖЕНИЯ

Было отмечено, что в поперечном сечении стержня действуют не сосредоточенные внутренние усилия N, Q, M_k и т. д., а непре­рывно распределенные силы, интенсивность которых может быть различной в разных точках сечения и в разном направлении.

Как же измерить интенсивность внутренних сил в данной точке данного сечения, например в точке В (рис. 6.1).

Выделим вокруг точки В малую площадку DA. Пусть – DR равнодей­ствующая внутренних сил, действую­щих на эту площадку.

Тогда среднее значение внутрен­них cил, приходящихся на единицу площади рассматриваемой площадки DA, будет равно

.

Величина р_ср называется средним напряжением. Она характеризует среднюю интенсивность внутренних сил. Уменьшая размеры площади, в пределе получим

p = .

Величина р называется истинным напряжением или просто напряжением в данной точке данного сечения. Упрощенно мож­но сказать, что напряжением называется внутренняя сила, при­ходящаяся на единицу площади в данной точке данного сечения.

Полное напряжение р можно разложить на две составляю­щие (рис. 6.2, а):

1) составляющую, нормальную к плоскости сечения. Эта составляющая обозначается s и называется нормальным напря­жением;

2) составляющую, лежащую в плоскости сечения. Эта со­ставляющая обозначается t и называется касательным напря­жением. Касательное напряжение в зависимости от действую­щих сил может иметь любое направление в плоскости сечения. Для удобства t представляют в виде двух составляющих по направлению координатных осей (рис. 6.2, б).

Принятые обозначения напряжений показаны на рис. 6.2, б.

У нормального напряжения ставится индекс, указывающий, какой координатной оси параллельно данное напряжение. Растягивающее нормальное напряжение считается положительным, сжимающее – отрицательным. Обозначения касательных на­пряжений снабжены двумя индексами: первый из них указыва­ет, какой оси параллельна нормаль к площадке действия данно­го напряжения, а второй – какой оси параллельно само напря­жение.

Разложение полного напряжения на нормальное и касатель­ное имеет определенный физический смысл. Нормальное напря­жение возникает, когда частицы материала стремятся отдалить­ся друг от друга или, наоборот, сблизиться. Касательные напря­жения связаны со сдвигом частиц материала по плоскости рассматриваемого сечения.

Тема №7. ОПРЕДЕЛЕНИЕ ВНУТРЕННИХ УСИЛИЙ

Рассмотрим случай осевого (центрального) растяжения или сжатия, когда внешние силы действуют по оси стержня (рис. 7.1). Для определения внутренних усилий (продольных сил) применим метод сечений.

Проведем какое-нибудь сечение, например а – а, и рассмот­рим равновесие нижней отсеченной части. Воздействие верхней отброшенной части на нижнюю заменим продольной силой и предварительно направим ее от сечения, т. е. предположим, что сила является растягивающей. Составим уравнение равнове­сия. Проецируя все силы, действующие на нижнюю часть, на направление параллельное оси стержня, и приравнивая сумму проекций нулю, получаем N₁ + 8Р – 5Р = 0, откуда N₁ = –3Р.

Знак минус показывает, что направление силы N₁ следует изменить на обратное, т. е. продольная сила будет в данном случае не растягивающей, как мы предположили, а сжимающей. Аналогично найдем продольную силу в сечении б – б: N₂ = 5Р (растяжение). Условимся продольную силу, соответствующую растяжению, считать положительной.

Наглядное представление о законе изменения продольных сил по длине стержня дает график (зпюра продольных сил), ось абсцисс которого проводится па­раллельно оси стержня, а ось ординат ей перпендикулярна. По оси ординат в выбранном мас­штабе откладывают значения про­дольных сил (с учетом знаков) в поперечных сечениях стержня. Для рассмотренного случая эпю­ра N представлена на рис. 7.1.

Тема №8. ОПРЕДЕЛЕНИЕ НАПРЯЖЕНИЙ

Если на поверхность призматического стержня нанести сетку линий, параллельных и перпендикулярных оси стержня (рис. 8.1, а), и приложить к нему растягивающую силу, то можно убедиться в том, что линии сетки и после деформации останутся взаимно перпендикулярными, за исключением небольшого участка стержня вблизи точки приложения силы, который из рас­смотрения пока исключаем, но расстояния между ними изме­нятся (рис. 8.2, б). Все горизонтальные линии, например cd, переместятся вниз, оставаясь горизонтальными и прямыми. Можно предположить также, что и внутри стержня будет такая же картина, т. е. поперечные сечения стержня, плоские и нор­мальные к его оси до деформации, останутся плоскими и нор­мальными к оси и после деформации.

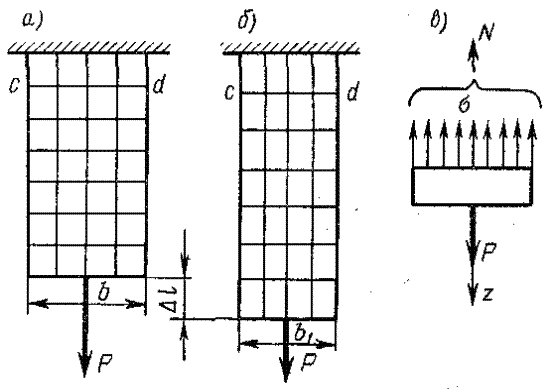
Эту гипотезу называют гипотезой плоских сечении или гипо­тезой Бернулли. Формулы, полученные на основе этой гипотезы, подтверждаются результатами опытов. Такая картина деформаций дает основание считать, что в поперечных сечениях стержня действуют только нормальные напряжения, равномерно распределенные по сечению, а каса­тельные напряжения равны нулю.

Продольная сила N есть равнодействующая нормальных напряжений в поперечном сечении:

N = òs dF.

Поскольку s = const, получим N = s∙F, откуда ;

В частном случае, когда на стержень действует одна внеш­няя сила Р, из уравнения равновесия получим N = Р (рис. 8.1, в) и вместо общей формулы получим частный вид форму­лы для растяжения

;

Эти формулы справедливы и для сжатия, с той только разни­цей, что сжимающие напряжения считаются отрицательными.

Кроме того, сжатые стержни помимо расчета на прочность рассчитываются также на устойчивость.

Тема №9. ОПРЕДЕЛЕНИЕ ДЕФОРМАЦИЙ И ПЕРЕМЕЩЕНИЙ

Для многих материалов при нагружении до определенных пределов опыты показывают следующую зависимость между относительным удлинением стержня e и напряжением s:

;

Эта зависимость носит название закона Гука и формулирует­ся следующим образом:

В формуле Е — коэффициент, зависящий от материала и называемый модулем продольной упругости или модулем упру­гости первого рода (модуль Юнга). Он характеризует жесткость материала, т. е. его способность сопротивляться деформированию.

Поскольку e – безразмерная величина, то из формулы видно, что единица Е та же, что и s, т. е. паскаль (Па).

Имея в виду, что для стержня постоянного сечения , а то можно получить формулу для определения полного (абсолютного) удлинения (укорочения) стержня:

Дата добавления: 2013-12-12