
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Метод экстраполяции по среднему темпу роста
|
|
|
|
Метод экстраполяции по среднему абсолютному приросту
Математические методы
Методы демографического прогнозирования
А. Методы экстраполяции – простейшие методы прогнозирования, основанные на предположении неизменности среднегодовых темпов роста, среднегодовых абсолютных и относительных приростов.
Методы экстраполяции применяются в демографии для расчёта общей численности населения только при отсутствии резких колебаний рождаемости, смертности и миграции.
Математическая модель по этому методу имеет вид линейной функции:
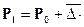 t, (7.1)
t, (7.1)
где 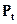 – прогнозируемый уровень численности населения;
– прогнозируемый уровень численности населения;
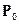 – базовый уровень численности населения;
– базовый уровень численности населения;
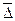 – абсолютный среднегодовой прирост численности населения;
– абсолютный среднегодовой прирост численности населения;
t – период прогнозирования.
В реальности неизменные среднегодовые абсолютные приросты могут оставаться таковыми только непродолжительное время, поэтому прогнозирование численности населения с использованием указанной линейной функции может быть использовано только в краткосрочных прогнозах.
Математическая модель по этому методу имеет вид степенной функции:
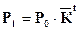 , (7.2)
, (7.2)
где: 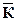 – среднегодовой коэффициент роста численности населения.
– среднегодовой коэффициент роста численности населения.
В этой модели предполагается ежегодное изменение численности населения в одно и то же число раз, т.е. его рост (или снижение) в
геометрической прогрессии.
От среднегодовых коэффициентов роста можно перейти к среднегодовым коэффициентам прироста, и тогда формулу (7.2) можно преобразовать следующим образом:
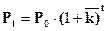 , (7.3)
, (7.3)
где 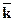 – среднегодовой коэффициент прироста населения.
– среднегодовой коэффициент прироста населения.
Путём преобразования формулы (7.3) можно определить период удвоения населения:
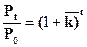 (7.4)
(7.4)
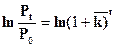 (7.5)
(7.5)
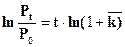 (7.6)
(7.6)
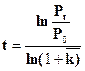 (7.7)
(7.7)
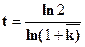 (7.8)
(7.8)
Соответственно, период сокращения населения вдвое будет определяться по следующей формуле:
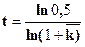 (7.9)
(7.9)
Задание 7.1. Известно, что коэффициент естественного прироста в населении Средней Азии составил 10%о (данные условные).
Требуется определить число лет, через которое численность населения увеличится в 2 раза при условии сохранения темпа роста и отсутствия миграции.
Решение:
Определим период удвоения населения данного региона, используя формулу 7.8:
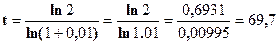 (лет).
(лет).
|
|
|
|
|
Дата добавления: 2013-12-12; Просмотров: 4774; Нарушение авторских прав?; Мы поможем в написании вашей работы!