Простая ставка процента

Часть 2

Курс лекций

Финансы, денежное обращение и кредит

Орлов Анатолий Александрович

Сводный план 2012 г., позиция

_________________________________________________________________

Подписано в печать Формат Тираж 100

Усл. печ. л. Заказ

127994, Москва, ул. Образцова, дом 9, стр.9. Типография МИИТа.

[1] не включая выплаты по долгу МВФ;

[2] прирост иностранных обязательств без учета изменений, связанных с прощением долгов;

[3] включая полученные капитальные трансферты, связанные с прощением долгов; включая выплаты по долгу МВФ;

[4] прирост иностранных активов без учета изменений, связанных с прощением долгов;

[5] включая выплаченные капитальные трансферты, связанные с прощением долгов.

[6] сумма показателей по статьям "торговые кредиты и авансы", "непоступление экспортной выручки" и “своевременно не погашенные импортные авансы”.

Если ставка процента применяется к постоянной исходной базе на протяжении всего периода договора, то говорят об использовании простой процентной ставки.

Под наращенной суммой ссуды (долга, депозита и т.д.) понимается ее первоначальная сумма вместе с начисленными на нее процентами к концу срока.

Наращенная сумма определятся умножением первоначальной суммы на множитель наращения, который показывает во сколько раз наращенная сумма больше первоначальной суммы.

Для записи формул используют следующие общепринятые обозначения:

I – проценты за весь срок

P – первоначальная сумма

S – наращенная сумма, т.е. P + I

i – ставка процента

Начисление процентов за один период: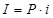

За n периодов: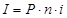

Процесс изменения суммы долга с начисление простых процентов описывается арифметической прогрессией, члены которой:

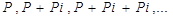
Формула для расчета наращенной суммы по простой процентной ставке имеет вид:

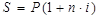
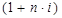- множитель наращения

* Примечание: выделяют три варианта расчета процентов:

1. точные проценты с точным числом дней ссуды (год – 365 дней, полугодие – 182 дня)
2. обыкновенные проценты с точным числом дней ссуды (банковский способ). Дает несколько больший результат, чем применение точных процентов (год – 360 дней)
3. обыкновенные проценты с приближенным числом дней ссуды. Используют, как правило, для промежуточных вычислений, не требующих абсолютной точности (месяц – 30 дней всегда).

Дифференцирование по простой ставке процента

Финансовый менеджер может столкнуться с задачей, обратной определению наращенной суммы – по заданной сумме S, которую следует уплатить через время n нужно определить сумму полученной ссуды, т.е. P.

Ситуация для такого рода расчетов – разработка условий контракта, удержание процентов сразу при выдаче ссуды и др.

В таких случаях говорят, что сумма S, дисконтируется, а сам процесс начисления и удержания процентов вперед наз. учетом.

Проценты в виде разницы S – P = D, наз. дисконтом

Термин «дисконтирование» употребляется и в более широком смысле – как средство определения любой стоимостной величины на некоторый момент времени при условии, что в будущем она составим величину S, вне зависимости от того, имела ли место финансовая операция, предусматривающая начисление процента или нет.

Величину P, найденную дисконтированием S, наз. приведенной (P’)

С помощью дисконтирования учитывается фактор времени. Формулу расчета величины P получаем из базовой ф. расчета наращенной суммы:

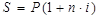, отсюда:

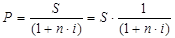(формула математического дисконтирования)

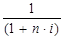- множитель дисконтирования. Показывает, какую долю составляет P в S.

* Примечание: если n ≠ целому числу лет, тогда:

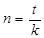
где t – число дней сделки

k – временная база, т.е. число дней в году

Определение продолжительности ссуды:

в годах:

1)

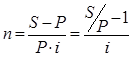
2)

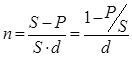
в днях:

3)

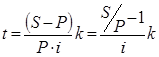
4)

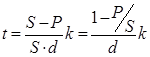
где d – учетная ставка

Дата добавления: 2013-12-12