Оценка точности равноточных измерений

Случайных ошибок

Классификация ошибок измерений. Свойства

ЭЛЕМЕНТЫ ТЕОРИИ ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЙ

При геодезических измерениях неизбежны ошибки. В измерительной практике различают грубые, систематические и случайные ошибки.

К грубым ошибкам относят просчеты в измерениях по причине невнимательности наблюдателя или неисправности прибора и они полностью должны быть исключены путем повторного измерения. Систематические ошибки происходят от известного источника, имеют определенный знак и величину и их можно учесть при измерениях и вычислениях. Влияние систематических ошибок на результат измерений сводится к минимуму путем введения поправки к результату измерения или применением соответствующей методики измерений.

Случайные ошибки имеют место при каждом измерении. Эти ошибки обусловлены точностью прибора, квалификацией наблюдателя, влиянием внешней среды, и полностью исключить из результатов измерений их нельзя. Закономерность таких ошибок проявляется лишь при большом числе измерений.

Так как случайные ошибки исключить из результатов измерений нельзя, то возникают две задачи: как из результатов измерений получить наиболее точную величину и как оценить точность полученных результатов измерений. Эти задачи можно разрешить с помощью теории ошибок измерений.

В основу теории ошибок положены следующие свойства случайных ошибок:

1. Малые ошибки встречаются чаще, а большие – реже.

2. Ошибки не превышают известного предела.

3. Положительные и отрицательные ошибки, одинаковые по абсолютной величине, одинаково часто встречаются.

4. Сумма ошибок деленная на число измерений, стремится к нулю при большом числе измерений.

Под равноточными измерениями понимают результаты, полученные при измерении одним и тем же прибором, одним и тем же равноценным методом и т. д. Оценку точности ряда равноточных измерений одной и той же случайной величины выполняют в определенном порядке.

Исходя из четвертого свойства случайных ошибок при геодезических измерениях одинаковой точности, за окончательный результат принимают средний результат из ряда измерений.

Если измерена одна и та же величина n раз и получены результаты: l ₁, l ₂, …, l _n, то

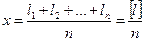. (4.2.1.)

Величина x называется арифметической срединой или вероятнейшим значением измеренной величины. Разности между каждым измерением и арифметической срединой называют вероятнейшими ошибками измерений:

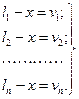(4.2.2.)

Сложив эти равенства, получим

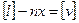. (4.2.3.)

Из формул (4.2.1.) и (4.2.3.) следует, что [ v ] =0

Точность результатов измерений оценивается средней квадратической ошибкой. Средняя квадратическая ошибка одного измерения вычисляется по формуле:

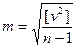(4.2.4.)

где [ v² ] – сумма квадратов вероятнейших ошибок; n – число измерений.

Средняя квадратическая ошибка арифметической средины вычисляется по формуле:

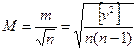. (4.2.5.)

Предельная ошибка не превышает утроенной средней квадратической ошибки, т. е.

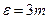. (4.2.6.)

Абсолютная ошибка m не всегда дает, полное представление о точности результатов измерений, поэтому пользуются относительной ошибкой

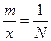. (4.2.7.)

4.3.Средняя квадратическая ошибка функций измеренных величин.

Если мы имеем функцию суммы или разности двух независимых величин

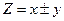; (4.3.1.)

то квадрат средней квадратической ошибки функции выразится формулой:

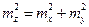; (4.3.2.)

При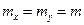

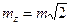. (4.3.3.)

Если функция имеет вид

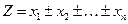, (4.3.4.)

то

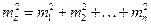, (4.3.5.)

т. е. квадрат средней квадратической ошибки алгебраической суммы аргументов равен сумме квадратов средних квадратических ошибок слагаемых.

Если ,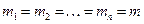

то

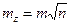, (4.3.6.)

т. е. средняя квадратическая ошибка алгебраической суммы измеренных с одинаковой точностью величин в 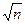раз больше средней квадратической ошибки одного слагаемого.

Если функция имеет вид

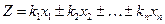, (4.3.7.)

то

, (4.3.8.)

где 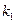, , 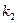…, 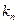– постоянные числа; 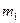, , 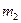…, 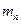– средние квадратические ошибки соответствующих аргументов.

Дата добавления: 2013-12-12