Вычисление координат вершин теодолитного хода

Прямая геодезическая задача.

Прямая и обратная геодезические задачи

Вычисление дирекционных углов и румбов сторон разомкнутого теодолитного хода

Угловая невязка разомкнутого теодолитного хода

Рис. 7.6.1. Схема обработки разомкнутого теодолитного хода

Координаты исходных точек А, В и С, D опорной сети и дирекционные углы a ₀ и a _n известны. Угловая невязка разомкнутого хода (рис. 7.6.1.) вычисляется по формуле

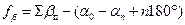(7.6.1.)

Координаты исходных точек A, B и C, D опорной сети и дирекционные углы α₀ и α_n (рис. 7.6.1.) известны. Из рисунка следует

,

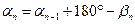т. е. дирекционный угол каждой последующей линии равен дирекционному углу предыдущей линии плюс 180°, минус вправо по ходу лежащий угол.

При вычислительной обработке результатов измерений на местности, при проектировании инженерных сооружений и перенесении их в натуру возникает необходимость решить прямую и обратную геодезические задачи (рис. 7.7.1.).

Рис. 7.7.1. Прямая и обратная геодезические задачи

Даны координаты x ₁ и y ₁ точки А начала линии АВ, ее горизонтальное проложение d и дирекционный угол a. Требуется определить координаты x ₂ и y ₂ точки В конца этой линии. Из рисунка видно, что координаты

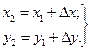(7.7.1.)

Разности координат конечной и начальной точек линии АВ, т. е. Dx и Dy называются приращениями координат:

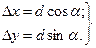(7.7.2.)

При помощи румбов приращения координат вычисляются по формулам:

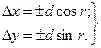(7.7.3.)

Приращения координат имеют знаки, которые зависят от знака косинуса и синуса дирекционного угла или от названия румба линии:

Румбы	СВ	ЮВ	ЮЗ	СЗ
Приращения:
Dx	+	-	-	+
Dy	+	+	-	-

Вычисление приращений координат выполняют с помощью таблиц натуральных значений sin и cos или с помощью вычислительных машин.

Обратная геодезическая задача. Даны координаты x ₁ и y ₁ точки А начала линии АВ и координаты x ₂, y ₂ точки В конца этой линии. Требуется определить длину и дирекционный угол или румб этой линии. Из рисунка следует, что

(7.7.4.)

или

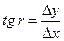, (7.7.5.)

r определяют по таблицам натуральных значений тригонометрических функций или с помощью микрокалькулятора. Название румба определяют по знакам Dy и Dx. По румбу можно вычислить дирекционный угол a.

Расстояние d вычисляется по формулам

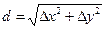(7.7.6.)

или

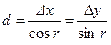. (7.7.7.)

Решая прямую геодезическую задачу вычисляют приращения координат вершин теодолитного хода, затем определяют невязки в приращениях координат.

Невязки в приращениях координат замкнутого полигона

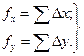(7.8.1.)

Вычисляется невязка в периметре

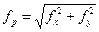. (7.8.2.)

Относительная невязка в периметре должна быть не больше допустимой

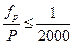, (7.8.3.)

где P – периметр полигона.

Если невязка в периметре допустима, то невязки f_x и f_y распределяют с обратным знаком соответственно на все приращения Dx и Dy пропорционально длинам сторон, для чего вычисляют поправки к приращениям по формулам

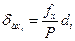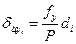; . (7.8.4.)

Сумма поправок должна равняться невязкам с обратным знаком.

После этого вычисляют исправленные приращения координат с контролем

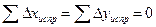. (7.8.5.)

Вычисляют координаты вершин полигона пользуясь правилом: координата последующей точки плюс соответствующее приращение, т. е.

, (7.8.6.)

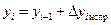. (7.8.7.)

Контроль – вторичное получение координат исходной вершины полигона.

Дата добавления: 2013-12-12