Итак, две величины υ и θ являются компонентами перемещения произвольного поперечного сечения балки

Рис.1.1

Дифференциальное уравнение изогнутой оси балки

КРАТКИЙ КУРС СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ

Часть 2

Учебное пособие

Санкт-Петербург 2010

УДК 539.3.8

Эйгенсон С.Н., Корихин Н.В., Шевелёв Л.П. Краткий курс сопротивления материалов. Часть 2: Учеб. пособие – СПб.: Изд-во ПИМаш, 2010. – 149 с.

Написано по материалам лекций, много лет читаемых авторами в Институте машиностроения (заводе – ВТУЗе). В сжатой форме изложены минимально необходимые сведения, соответствующие программе машиностроительных вузов.

Во второй части пособия излагаются следующие разделы курса сопротивления материалов: перемещения балок при изгибе, статически неопределимые балки, сложное сопротивление, устойчивость сжатых стержней, усталость, динамические нагрузки.

Для студентов вузов машиностроительного профиля. Особенно рекомендуется студентам вечерней и заочной форм обучения.

Ил. – 95, табл. – 6, библиогр. – 7 назв.

Рецензенты: д-р техн. наук, проф. В.В.Улитин (СПбГУНТ и ПТ)

д-р техн. наук, проф. И.А.Богов (ПИМаш)

Ó Санкт-Петербургский

институт машиностроения, 2010

Глава 1. ПЕРЕМЕЩЕНИЯ БАЛОК ПРИ ИЗГИБЕ

Для того чтобы судить о работе балок, недостаточно знать только напряжения, возникающие в сечениях балки от заданной нагрузки.

Напряжения позволяют проверить прочность, однако прочные балки могут оказаться непригодными к эксплуатации из-за недостаточной жёсткости. Для проверки жёсткости балки необходимо научиться определять перемещения отдельных точек её оси.

а б

На рис.1.1,а показана балка, заделанная одним концом и нагруженная сосредоточенной силой. В результате изгиба ось становится криволинейной. Точка К перемещается в положение К′. Вертикальная составляющая этого перемещения – υ_max, горизонтальная – u_max, угол наклона касательной – θ_max.

Следует отметить, что υ – это перемещение центра тяжести сечения вдоль оси у, а расстояние произвольной точки поперечного сечения от нейтральной оси z – это у (см. рис.1.1,б).

Подавляющее большинство балок, используемых в технике (валы турбин, электрических машин, мосты и пр.), очень жёсткие. Их наибольший прогиб υ_max не должен превышать 1/400 ¸ 1/1000 длины пролёта ℓ. При этом получается, что горизонтальное перемещение u меньше 1/100 ¸ 1/10000 от υ, поэтому считаем, что u = 0.

При малых прогибах υ угол наклона касательной к оси θ можно определить с помощью выражения

θ @ 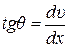. (1.1)

Связь между кривизной изогнутой оси и изгибающим моментом была получена при выводе формулы нормальных напряжений при изгибе – см. п.5.4, формула (5.17):

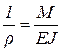. (1.2)

Известно также из математического анализа уравнение кривизны плоской кривой

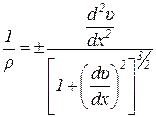. (1.3)

Приравняв правые части формул (1.2) и (1.3), получим дифференциальное уравнение изогнутой оси. Учитывая отмеченную выше малость прогибов и углов наклона касательной, можно пренебречь квадратом первой производной в знаменателе 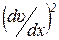по сравнению с единицей. Тогда получим приближённое дифференциальное уравнение изогнутой оси

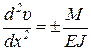. (1.4)

Знак зависит от направления осей координат. Если ось 0υ направлена вверх, знаки кривизны и изгибающего момента совпадают (рис.1.2), поэтому в уравнении (1.4) берётся знак «+».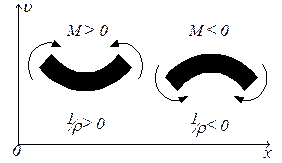

Рис. 1.2

Если ось 0υ направлена вниз, то знаки кривизны и изгибающего момента различны, поэтому в правой части уравнения (1.4) берётся знак «–».

Впредь ось 0υ будем всегда направлять вверх; дифференциальное уравнение изогнутой оси имеет следующий вид

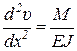. (1.5)

Уравнение (1.5) выведено для случая чистого изгиба (М = const, Q = 0), но используется и для случая поперечного изгиба (Q ¹ 0). Учитывая дифференциальные зависимост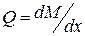и и 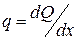(см. п. 5.2 первой части курса), отметим физический смысл функции υ и её производных:

υ – прогиб в произвольном сечении балки;

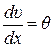– угол поворота произвольного сечения балки;

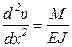– изгибающий момент, делённый на жёсткость;

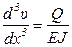– поперечная сила, делённая на жёсткость;

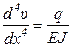– интенсивность распределённой нагрузки, делённая на жёсткость.

Дата добавления: 2013-12-11