
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Средняя гармоническая
|
|
|
|
Лекция 7. виды и свойства средних в статистике
4.6. Средняя гармоническая.
4.7. Средняя геометрическая, средняя квадратическая, средняя хронологическая.
4.8. Структурные средние.
4.9. Робастные характеристики для оценки среднего арифметического
Среднюю арифметическую мы рассмотрели в предыдущей лекции. Наряду со средней арифметической, в статистике применяется средняя гармоническая величина, обратная средней арифметической из обратных значений признака. Как и средняя арифметическая, она может быть простой и взвешенной.
Средняя гармоническая величина является преобразованной средней арифметической величиной.
Рассмотрим следующий пример.
Бригада токарей была занята обточкой одинаковых деталей в течение 8-часового рабочего дня. Первый токарь затратил на одну деталь 12 мин, второй - 15 мин., третий - 11, четвертый - 16 и пятый - 14 мин. Определите среднее время, необходимое на изготовление одной детали.
На первый взгляд кажется, что задача легко решается по формуле средней арифметической простой:
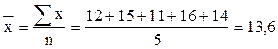
Полученная средняя была бы правильной, если бы каждый рабочий сделал только по одной детали. Но в течение дня отдельными рабочими было изготовлено различное число деталей. Для определения числа деталей, изготовленных каждым рабочим, воспользуемся следующим соотношением:
все затраченное время
Среднее время, затраченное = --------------------------------------
на одну деталь число деталей
Число деталей, изготовленных каждым рабочим, определяется отношением всего времени работы к среднему времени, затраченному на одну деталь. Тогда среднее время, необходимое для изготовления одной детали, равно:
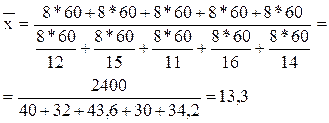
Это же решение можно представить иначе:
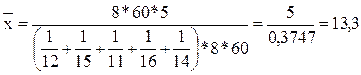
Таким образом, формула для расчета средней гармонической простой будет иметь вид:
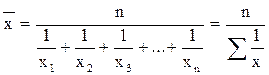
Средняя гармоническая взвешенная применяется тогда, когда необходимые веса (частоты - ni) в исходных данных не заданы непосредственно, а входят сомножителем в одни из имеющихся показателей, являющихся весовыми коэффициентами для вариант.
Рассмотрим следующий пример.
Издержки производства и себестоимость единицы продукции А по трем заводам характеризуются следующими данными:
Таблица 27
| Номер завода | Издержки производства, тыс.руб. | Себестоимость единицы продукции, руб. |
Исчислим среднюю себестоимость изделия по трем заводам. Как и прежде, главным условием выбора формы средней является экономическое содержание показателя и исходные данные.
Издержки производства
Средняя себестоимость = ----------------------------------------
единицы продукции (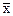 ) Количество продукции
) Количество продукции
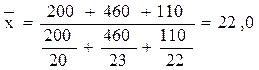 руб.
руб.
Таким образом, формулу для расчета средней гармонической взвешенной можно представить в общем виде:
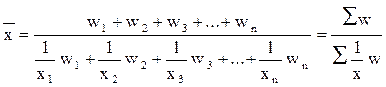
Общее условие применения средней гармонической: к средней гармонической следует прибегать в тех случаях, когда в качестве весов применяются не численности единиц совокупности а произведения эти частот на значение признака (т.е. w = xf)
|
|
|
|
Дата добавления: 2013-12-11; Просмотров: 300; Нарушение авторских прав?; Мы поможем в написании вашей работы!