Понятие предельной ошибки выборки

Определение ошибки выборочной доли.

При повторном отборе средняя ошибка выборочной доли рассчитывается по формуле:

,

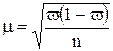где 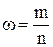— выборочная доля единиц, обладающих изучаемым признаком;

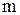— число единиц, обладающих изучаемым признаком;

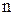— численность выборки.

При бесповторном способе отбора средняя ошибка выборочной доли определяется по формулам:

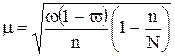
Тот факт, что генеральная средняя (или генеральная доля) не выйдет за определенные пределы, можно утверждать не с абсолютной достоверностью, а лишь с определенной степенью вероятности.

Значит, с определенной степенью вероятности, мы можем утверждать, что отклонения выборочных характеристик от генеральных не превысят некоторой величины, которая называется предельной ошибкой выборки.

Предельная ошибка выборки 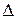связана со средней ошибкой выборки 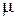отношением:

.

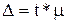При этом t как коэффициент кратности средней ошибки выборки (так называемый, коэффициент доверия) зависит от значения вероятности Р, с которой гарантируется величина предельной ошибки выборки.

Предельная ошибка выборки при бесповторном отборе определяется по следующим формулам:

,

.

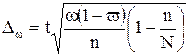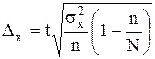Предельная ошибка выборки при повторном отборе определяется по формуле:

,

.

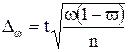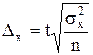Таблица 45

Значение вероятности при разной величине коэффициента доверия t.

t	вероятность	t	вероятность	t	вероятность
1,0	0,6827	1,8	0,9281	2,5	0,9876
1,1	0,7287	1,9	0,9426	2,58	0,9900
1,2	0,7699	1,96	0,9500	2,6	0,9907
1,3	0,8064	2,0	0,9545	2,7	0,9931
1,4	0,8385	2,1	0,9643	2,8	0,9949
1,5	0,8664	2,2	0,9722	2,9	0,9963
1,6	0,8904	2,3	0,9786	3,0	0,9973
1,7	0,9109	2,4	0,9836	3,28	0,9990

Последнее замечание относится к дисперсии. В математической статистике доказано, что соотношение между генеральной дисперсией и выборочной такое:

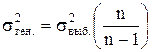
Дата добавления: 2013-12-11