Непараметрические методы изучения связей

Наиболее простым из них является вычисление коэффициента знаков Фехнера. Он рассчитывается по формуле:

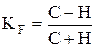
C - сумма совпадающих знаков отклонений индивидуальных значений признака от средней.

H - сумма несовпадений

Данный коэффициент изменяется в пределах (-1;1).

Значение KF=0 свидетельствует об отсутствии зависимости между изучаемыми признаками.

Если KF=±1, то это говорит о наличии функциональной прямой (+) и обратной (-) зависимости. При значении KF>½0,6½ делается вывод о наличии сильной прямой (обратной) зависимости между признаками.

Их еще называют ранговыми методами. Они связаны с расчетами различных коэффициентов. Применяются как отдельно, так и совместно с параметрическими. Особенно эффективны непараметрические методы, когда необходимо измерить связь между качественными признаками. Они проще в вычислении и не требуют никаких предположений о законе распределения исходных статистических данных, т.к. при их расчете оперируют не самими значениями признаков, а их рангами, частотами, знаками и т.д.

Коэффициенты ассоциации и контингенции

Для исследования взаимосвязи качественных альтернативных признаков, принимающих только 2 взаимоисключающих значения и состоящих только из двух групп, используется коэффициенты ассоциации и контингенции. При расчете этих коэффициентов составляется т.н. таблица 4-х камней.

Рассмотрим пример:

Таблица 54

Посещение	Оценка	Итого
Неудовлетв.	Положит.
Посещали
Не посещали
Итого

Перепишем данную таблицу, заменив обозначениями:

Таблица 55

Посещение	Оценка	Итого
Неудовлетв.	Положит.
Посещали	a	b	a + b
Не посещали	с	d	c + d
Итого	a + c	b + d	a + b+ c+ d

Вычислим следующие коэффициенты:

1) коэффициент ассоциации

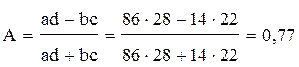
2 ) коэффициент контингенции

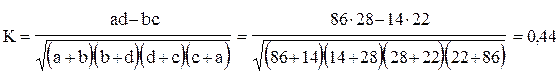
Коэффициент контингенции всегда меньше коэффициента ассоциации. Связь считается подтвержденной, ес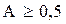ли или .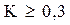

Если признаки имеют 3 или более градаций, то для изучения взаимосвязей используются коэффициенты Пирсена и Чупрова. Они рассчитываются по формулам:

С - коэффициент Пирсена

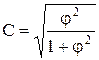
К - коэффициент Чупрова

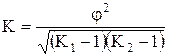
j - показатель взаимной сопряженности

K₁ - число значений (групп) первого признака

K₂ - число значений (групп) второго признака

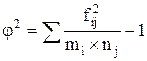
f_ij - частоты соответствующих клеток таблицы

m_i - столбцы таблицы

n_j - строки

Для расчета коэффициентов Пирсена и Чупрова составляется вспомогательная таблица:

Таблица 56

Группа признака Y	Группа признака X	Итого:
		...	i
	f11	f12	...	f1i	n1
	f21	f22	...	f2i	n2
...	...	...	...	...	...
j	fji	fj2	...	fji	nj
Итого:	m1	m2	...	mi	SSminj

При ранжировании качественных признаков с целью изучения их взаимосвязи используется коэффициент корреляции Кэндалла.

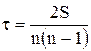
n - число наблюдений

S - сумма разностей между числом последовательностей и числом инверcий по второму признаку.

S=P+Q

P - сумма значений рангов, следующих за данными и превышающих его величину

Q - сумма значений рангов, следующих за данными и меньших его величины (учитывается со знаком «-»).

При наличии связанных рангов формула коэффициента Кендалла будет следующей:

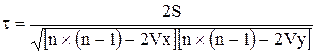
Vx и Vy определяются отдельно для рангов X и Y по формуле:

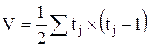
Коэффициент Спирмана (ранговый коэффициент)

Один из простых показателей тесноты корреляционной зависимости — показатель корреляции рангов. Разберем порядок вычисления этого показателя на примере.

Изучается товарооборот и суммы издержек обращения по ряду магазинов (в тыс. руб.). Данные представлены таблицей.

Таблица 57

№ магазина	Товарооборот	Издержки обращения

Из таблицы видно, что с ростом товарооборота растут и издержки обращения.

Но в ряде случаев, как видно из той же таблицы, увеличение товарооборота ведет и к уменьшению издержек обращения, поскольку, помимо двух названных величин, в реальном процессе торговли участвуют и другие факторы, которые в рассмотрение не включены и носят случайный характер.

Рассмотрим критерий тесноты связи, названный показателем корреляции рангов. От величин абсолютных перейдем к рангам по такому правилу: самое меньшее значение — ранг 1, затем 2 и т.д. Если встречаются одинаковые значения, то каждое из них заменяется средним.

Итак:

Товарооборот	Издержки
	7,5
	7,5

Построим разности между рангами и возведем их в квадрат.

1. Если ранги совпадают, то ясно, что сумма их квадратов равна 0.

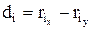
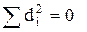
Связь полная, прямая.

2. Ранги образуют обратную последовательность

1 10

2 9 В этом случае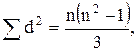

3 8

.. Связь полная, обратная.

..

..

10 1

Показатель корреляции рангов определяется по формуле:

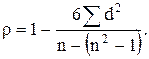
Показатель показывает, как отличается полученная при наблюдении сумма квадратов разностей между рангами от случая отсутствия связи.

Проанализируем показатель корреляции рангов.

1. Связь полная и прямая, 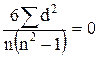и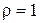

2. Связь полная и обратная, 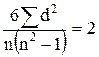и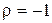

3. Все остальные значения лежат между -1 и +1.

Построим показатель корреляции рангов для нашего примера:

Таблица 58

Товарооборот (ранг)	Издержки (ранг)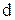
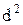
		-3
		-2
	7,5	-0,5	0,25
	7,5	0,5	0,25

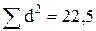
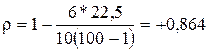
Полученный показатель свидетельствует о достаточно тесной связи между товарооборотом и издержками.

Дата добавления: 2013-12-11