Показатели тесноты статистической связи

Степень тесноты факторной и результативной переменной в корреляционно-регрессионном анализе можно определить с помощь специальных измерителей:

а) коэффициент детерминации;

б) эмпирическое корреляционное отношение (или индекс корреляции);

в) линейного коэффициента корреляции.

Коэффициент детерминации (по аналогии с тем как оценивалось соотношение межгрупповой и общей дисперсии, см. тема 5) вычисляется как отношение дисперсии совокупности теоретических значений 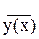(будем далее их обозначать y_x) к дисперсии совокупности наблюденных значений y:

или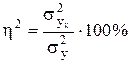

Так как изменчивость (дисперсия) совокупности y обусловлена всеми действующими факторами, а изменчивость (дисперсия) совокупности y_x только фактором x, то коэффициент детерминации покажет долю вклада данного фактора в общую изменчивость явления, т.е. в какой мере он им определяется и взаимосвязан с ним.

Корень квадратный из коэффициента детерминации называется индексом корреляции или корреляционным отношением.

Пользуясь формулой сложения дисперсий можно поучить и другие выражения для индекса корреляции:

Данный показатель изменяется от 0 до1 и по степени близости к 1можно судить на сколько данная связь по свое силе приближается к связи функциональной. При - связь полностью отсутствует, при - полная функциональная связь.

Наряду с построением и решением уравнения связи определяется степень тесноты этой связи при помощи линейного коэффициента корреляции, как частного случая общего индекса корреляции для прямолинейной зависимости между факторной и результативной переменной. На практике используется несколько формул, дающих одно и тоже значение для вычисления данного коэффициента:

Это коэффициент принимает как отрицательные (для обратной зависимости), так и положительные (для прямой зависимости) значения.

Коэффициент корреляции изменяется от -1 до +1 и показывает тесноту и направление корреляционной связи.

Если отклонения 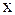по и по 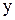от среднего совпадают и по знаку, и по величине, то это полная прямая связь, то =+1.

Если полная обратная связь, то =-1.

Если связь отсутствует, то =0.

Для установления тесноты связи с помощью коэффициента корреляции можно пользоваться шкалой Чеддока:

Величина коэффициента корреляции	Параметры связи
До – 0,3	Связь отсутствует
От ±0,3 до ±0,5	Связь слабая
От ±0,5 до ±0,7	Связь умеренная
До ±1	Связь сильная

Удобной формой изучения связи является корреляционная таблица. В этой таблице одни признаки располагаются по строкам, а другие – в колонках. Числа, стоящие на пересечении строк и колонок, показывают, сколько раз встречается данное значение факторного признака с данным значением результативного. Рассмотрим следующую схему:

Таблица 59

Часы простоя в неделю	Количество станков в цехах	fy
3-5	5-7	7-9	9-11
10-15
15-20
20-25
25-30
30-35
fx

По такой таблице можно сделать выводы (1) о том, существует ли связь, (2) о ее направлении и (3) о ее интенсивности (при условии существования связи).

Дата добавления: 2013-12-11