Гетероскедастичность

Одной из ключевых предпосылок МНК является условие постоянства дисперсий случайных отклонений для любых наблюдений. Выполнимость данной предпосылки называется гомоскедастичностью; невыполнимость данной предпосылки называется гетероскедастичностью.

В качестве примера реальной гетероскедастичности можно сказать, что люди с большим доходом не только тратят в среднем больше, чем люди с меньшим доходом, но и разброс в их потреблении также больше, поскольку они имеют больше простора для распределения дохода.

При гетероскедастичности последствия применения МНК будут следующими:

1. Оценки параметров останутся по-прежнему несмещенными и линейными.

2. Оценки не будут эффективными, т.е. не будут иметь наименьшую дисперсию по сравнению с другими оценками данного параметра. Они не будут даже асимптотически эффективными. Увеличение дисперсии оценок снижает вероятность получения максимально точных оценок.

3. Дисперсии оценок параметров будут рассчитываться со смещением.

4. Все выводы, получаемые на основе соответствующих t – и F – статистик, а также интервальные оценки будут ненадежными. Вполне вероятно, что стандартные ошибки коэффициентов будут занижены, а t – статистики завышены. Это может привести к признанию статистически значимыми коэффициентов, которые таковыми на самом деле не являются.

В ряде случаев, зная характер исходных данных, можно предвидеть гетероскедастичность и попытаться устранить её ещё на стадии спецификации. Однако значительно чаще эту проблему приходится решать после построения уравнения регрессии.

Графическое построение отклонений от эмпирического уравнения регрессии позволяет визуально определить наличие гетероскедастичности. В этом случае по оси абсцисс откладываются значения объясняющей переменной x_i (для парной регрессии) либо линейную комбинацию объясняющих переменных:

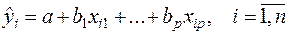
(для множественной регрессии), а по оси ординат либо отклонения e_i, либо их квадраты .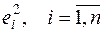

Если все отклонения 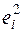находятся внутри горизонтальной полосы постоянной ширины, это говорит о независимости дисперсий 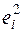от значений объясняющей переменной и выполнимости условия гомоскедастичности.

В других случаях наблюдаются систематические изменения в соотношениях между значениями 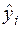и квадратами отклонений :

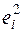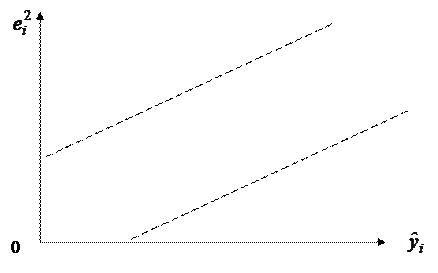Такие ситуации отражают большую вероятность наличия гетероскедастичности для рассматриваемых статистических данных.

В настоящее время для определения гетероскедастичности разработаны специальные тесты и критерии для них.

Тест ранговой корреляции Спирмена. При использовании данного теста предполагается, что дисперсия отклонений будет либо увеличиваться, либо уменьшаться с увеличением значений х. Поэтому для регрессии, построенной по МНК, абсолютные величины отклонений | e_i | и значения x_i будут коррелированы. Затем определяется коэффициент ранговой корреляции:

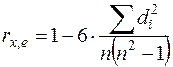, (53)

где d_i - разность между рангами x_i и | e_i |, n – число наблюдений. Например, если х₂₀ является 25 – м по величине среди всех значений х, а e₂₀ является 32 – м, то d₂₀ = 25 – 32 = -7.

Доказано, что при справедливости нуль – гипотезы 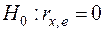статистика

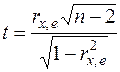(54)

имеет распределение Стьюдента с числом степеней свободы (n -2). Поэтому, если наблюдаемое значение статистики (54) превышает критическое 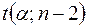, вычисленное по таблице критических точек распределения Стьюдента (двусторонних), то гипотезу о равенстве нулю коэффициента корреляции (53) следует отклонить и признать наличие гетероскедастичности. В противном случае нуль – гипотеза, которая соответствует отсутствию гетероскедастичности, принимается.

В модели множественной регрессии проверка нуль – гипотезы может осуществляться с помощью t – статистики по каждому фактору отдельно.

Тест Голдфелда – Квандта. В данном случае предполагается, что стандартное отклонение пропорционально значению переменной x_j, т.е. 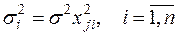. Предполагается, что остатки имеют нормальное распределение и отсутствует автокорреляция остатков.

Тест состоит в следующем:

1. Все n наблюдений упорядочиваются по величине x_j.

2. Вся упорядоченная выборка разбивается на три подвыборки размерностей k, n-2k и k соответственно.

3. Оцениваются отдельные регрессии для первой подвыборки (k первых наблюдений) и для третьей подвыборки (k последних наблюдений). Если предположение о пропорциональности дисперсий отклонений значениям x_j верно, то остаточная СКО по первой регрессии

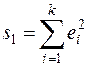
будет существенно меньше остаточной СКО по третьей регрессии

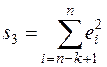
4. Для сравнения соответствующих дисперсий выдвигается нуль – гипотеза в виде

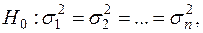
которая предполагает отсутствие гетероскедастичности. Для проверки нуль – гипотезы строится следующая статистика

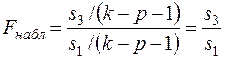(55)

которая при справедливости нуль – гипотезы имеет распределение Фишера с (k-p-1, k-p-1) степенями свободы.

5. Если

,

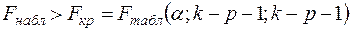то гипотеза об отсутствии гетероскедастичности отклоняется на уровне значимости α.

По рекомендациям специалистов, объем исключаемых данных k должен быть примерно равен четверти общего объёма выборки n.

Этот же тест может быть использован и при предположении об обратной пропорциональности между дисперсией и значениями объясняющей переменной. В этом случае статистика Фишера принимает вид:

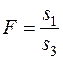(56)

При установлении гетероскедастичности возникает необходимость преобразования модели с целью устранения данного недостатка. Вид преобразования зависит от того, известны или нет дисперсии отклонений .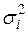

В случае, если дисперсии отклонений известны для каждого наблюдения, применяется метод взвешенных наименьших квадратов (ВНК). Гетероскедастичность устраняется, если разделить каждое наблюдаемое значение на соответствующее ему значение дисперсии.

Рассмотрим для простоты ВНК на примере парной регрессии:

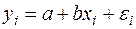(57)

Разделим обе части (57) на известное :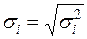

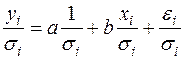(58)

Сделаем замены переменных:

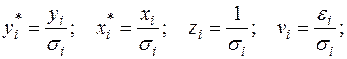(59)

получим уравнение регрессии без свободного члена, но с двумя факторами и с преобразованным отклонением:

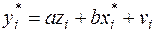(60)

Можно показать, что для v_i выполняется условие гомоскедастичности. Поэтому для модели (60) выполняются все предпосылки МНК, и оценки, полученные по МНК, будут наилучшими линейными несмещенными оценками.

Таким образом, наблюдения с наименьшими дисперсиями получают наибольшие «веса», а наблюдения с наибольшими дисперсиями – наименьшие «веса». Поэтому наблюдения с меньшими дисперсиями отклонений будут более значимыми при оценке параметров регрессии, чем наблюдения с большими дисперсиями. При этом повышается вероятность получения более точных оценок.

Полученные по МНК оценки параметров модели (60) можно использовать в первоначальной модели (57).

Для применения ВНК необходимо знать фактические значения дисперсий отклонений 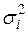. На практике такие значения известны крайне редко. Поэтому, чтобы применить ВНК, необходимо сделать реалистические предположения о значениях 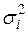. Чаще всего предполагается, что дисперсии отклонений пропорциональны или значениям x_i, или значениям .

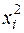Если предположить, что дисперсии пропорциональны значениям фактора x, т.е.

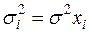(61)

тогда уравнение (57) преобразуется делением его левой и правой частей на :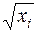

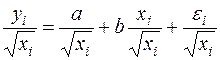
или

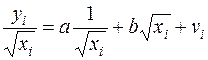(62)

Здесь для случайных отклонений 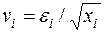выполняется условие гомоскедастичности. Следовательно, для регрессии (62) применим обычный МНК. Следует отметить, что регрессия (62) не имеет свободного члена, но зависит от двух факторов. Оценив для (62) по МНК коэффициенты а и b, возвращаемся к исходному уравнению регрессии.

Если в уравнении регрессии присутствует несколько объясняющих переменных, вместо конкретной переменной x_j используется исходное уравнение множественной регрессии

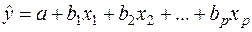
т.е. фактически линейная комбинация факторов. В этом случае получают следующую регрессию:

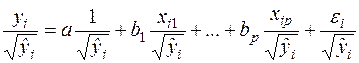(63)

Если предположить, что дисперсии 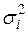пропорциональны 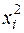, то соответствующим преобразованием будет деление уравнения регрессии (57) на x_i:

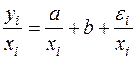
или, если переобозначить остатки как :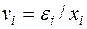

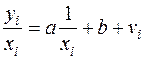(64)

Здесь для отклонений v_i также выполняется условие гомоскедастичности. Применяя обычный МНК к регрессии (64) в преобразованных переменных

,

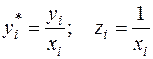получим оценки параметров, после чего возвращаемся к исходному уравнению (57). Отметим, что в регрессии (64) по сравнению с исходным уравнением параметры поменялись ролями: свободный член а стал коэффициентом, а коэффициент b – свободным членом.

Дата добавления: 2013-12-11