Динамические эконометрические модели

Таблица 3.

Таблица 2.

Таблица 1.

№ квартала	Потребление электроэнергии yt	Итого за четыре квартала	Скользящая средняя за четыре квартала	Центрированная скользящая средняя	Оценка сезонной компоненты
	6,0
	4,4
	5,0	24,4	6,10	6,25	-1,250
	9,0	25,6	6,40	6,45	2,550
	7,2	26,0	6,50	6,625	0,575
	4,8	27,0	6,75	6,875	-2,075
	6,0	28,0	7,00	7,1	-1,100
	10,0	28,8	7,20	7,3	2,700
	8,0	29,6	7,40	7,45	0,550
	5,6	30,0	7,50	7,625	-2,025
	6,4	31,0	7,75	7,875	-1,475
	11,0	32,0	8,00	8,125	2,875
	9,0	33,0	8,25	8,325	0,675
	6,6	33,6	8,40	8,375	-1,775
	7,0	33,4	8,35
	10,8

Шаг 2. Найдем оценки сезонной компоненты как разность между фактическими уровнями ряда (колонка 2 таблицы 1) и центрированными скользящими средними (колонка 5). Эти значения помещаем в колонку 6 таблицы 1 и используем для расчета значений сезонной компоненты (таблица 2), которые представляют собой средние за каждый квартал (по всем годам) оценки сезонной компоненты S_i. В моделях с сезонной компонентой обычно предполагается, что сезонные воздействия за период (в данном случае – за год) взаимопогашаются. В аддитивной модели это выражается в том, что сумма значений сезонной компоненты по всем точкам (здесь – по четырем кварталам) должна быть равна нулю.

Показатели	Год	№ квартала, i
I	II	III	IV
		-	-	-1,250	2,550
	0,575	-2,075	-1,100	2,700
	0,550	-2,025	-1,475	2,875
	0,675	-1,775	-	-
Итого за i – й квартал (за все годы)		1,800	-5,875	-3,825	8,125
Средняя оценка сезонной компоненты для i – го квартала,	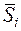	0,600	-1,958	-1,275	2,708
Скорректированная сезонная компонента,	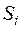	0,581	-1,977	-1,294	2,690

Для данной модели сумма средних оценок сезонной компоненты равна:

0,6-1,958-1,275+2,708=0,075.

Эта сумма оказалась не равной нулю, поэтому каждую оценку уменьшим на величину поправки, равной одной четверти полученного значения:

Δ=0,075/4=0,01875.

Рассчитаем скорректированные значения сезонной компоненты (они записаны в последней строке таблицы 2):

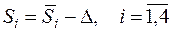(8)

Эти значения при суммировании уже равны нулю:

0,581-1,977-1,294+2,69=0.

Шаг 3. Исключаем влияние сезонной компоненты, вычитая её значения из каждого уровня исходного временного ряда. Получаем величины:

T+E=Y-S (9)

Эти значения рассчитываются в каждый момент времени и содержат только тенденцию и случайную компоненту (колонка 4 следующей таблицы):

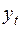
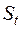
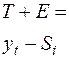
t				T	T+S		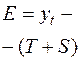E^2
	6,0	0,581	5,419	5,902	6,483	-0,483	0,2332
	4,4	-1,977	6,377	6,088	4,111	0,289	0,0833
	5,0	-1,294	6,294	6,275	4,981	0,019	0,0004
	9,0	2,69	6,310	6,461	9,151	-0,151	0,0228
	7,2	0,581	6,619	6,648	7,229	-0,029	0,0008
	4,8	-1,977	6,777	6,834	4,857	-0,057	0,0032
	6,0	-1,294	7,294	7,020	5,726	0,274	0,0749
	10,0	2,69	7,310	7,207	9,897	0,103	0,0107
	8,0	0,581	7,419	7,393	7,974	0,026	0,0007
	5,6	-1,977	7,577	7,580	5,603	-0,003	0,0000
	6,4	-1,294	7,694	7,766	6,472	-0,072	0,0052
	11,0	2,69	8,310	7,952	10,642	0,358	0,1278
	9,0	0,581	8,419	8,139	8,720	0,280	0,0785
	6,6	-1,977	8,577	8,325	6,348	0,252	0,0634
	7,0	-1,294	8,294	8,512	7,218	-0,218	0,0474
	10,8	2,69	8,110	8,698	11,388	-0,588	0,3458

Шаг 4. Определим трендовую компоненту данной модели. Для этого проведем выравнивание ряда (Т+Е) с помощью линейного тренда:

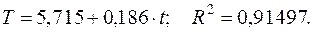
Подставляя в это уравнение значения 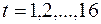, найдем уровни Т для каждого момента времени (колонка 5 таблицы 3).

Шаг 5. Найдем значения уровней ряда, полученные по аддитивной модели. Для этого прибавим к уровням Т значения сезонной компоненты для соответствующих кварталов, т.е. к значениям в колонке 5 таблицы 3 прибавим значения в колонке 3. Результаты операции представлены в колонке 6 таблицы 3.

Шаг 6. В соответствии с методикой построения аддитивной модели расчет ошибки производим по формуле:

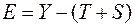(10)

Это абсолютная ошибка. Численные значения абсолютных ошибок приведены в колонке 7 таблицы 3.

По аналогии с моделью регрессии для оценки качества построения модели или для выбора наилучшей модели можно применять сумму квадратов полученных абсолютных ошибок. Для данной аддитивной модели сумма квадратов абсолютных ошибок равна 1,10. По отношению к общей сумме квадратов отклонений уровней ряда от его среднего уровня, равной 71,59, эта величина составляет чуть более 1,5%. Следовательно, можно сказать, что аддитивная модель объясняет 98,5% общей вариации уровней временного ряда потребления электроэнергии за последние 16 кварталов.

Пример. Построение мультипликативной модели временного ряда. Пусть имеются поквартальные данные о прибыли компании за последние четыре года:

Таблица 4.

Квартал     Год	I	II	II	IV

График временного ряда свидетельствует о наличии сезонных колебаний периодичностью 4 квартала и общей убывающей тенденции уровней ряда:

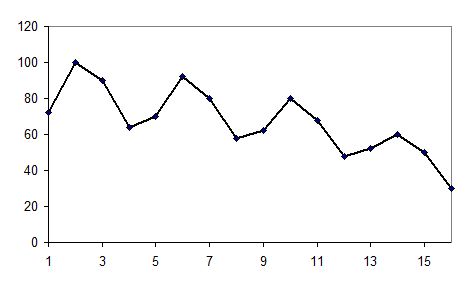Прибыль компании в весенне – летний период выше, чем в осенне – зимний период. Поскольку амплитуда сезонных колебаний уменьшается, можно предположить существование мультипликативной модели. Определим её компоненты.

Шаг 1. Проведем выравнивание исходных уровней ряда методом скользящей средней. Методика, применяемая на этом шаге, полностью совпадает с методикой аддитивной модели. Результаты расчетов оценок сезонной компоненты представлены в таблице:

Таблица 5.

№ квартала	Прибыль компании	Итого за четыре квартала	Скользящая средняя за четыре квартала	Центрированная скользящая средняя	Оценка сезонной компоненты
			81,500	81,250	1,108
			81,000	80,000	0,800
			79,000	77,750	0,900
			76,500	75,750	1,215
			75,000	74,000	1,081
			73,000	71,500	0,811
			70,000	68,500	0,905
			67,000	65,750	1,217
			64,500	63,250	1,075
			62,000	59,500	0,807
			57,000	54,750	0,950
			52,500	50,250	1,194
			48,000

Шаг 2. Найдем оценки сезонной компоненты как частное от деления фактических уровней ряда на центрированные скользящие средние (колонка 6 таблицы). Используем эти оценки для расчета значений сезонной компоненты S. Для этого найдем средние за каждый квартал оценки сезонной компоненты S_i. Взаимопогашаемость сезонных воздействий в мультипликативной модели выражается в том, что сумма значений сезонной компоненты по всем кварталам должна равняться числу периодов в цикле. В нашем случае число периодов одного цикла (год) равно четырем кварталам. Результаты расчетов сведем в таблицу:

Таблица 6.

Показатели	Год	№ квартала, i
I	II	III	IV
		-	-	1,108	0,800
	0,900	1,215	1,081	0,817
	0,905	1,217	1,075	0,807
	0,950	1,194	-	-
Итого за i – й квартал (за все годы)		2,755	3,626	3,264	2,424
Средняя оценка сезонной компоненты для i – го квартала,	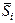	0,918	1,209	1,088	0,808
Скорректированная сезонная компонента,	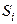	0,913	1,202	1,082	0,803

Здесь сумма средних оценок сезонных компонент по всем четырем кварталам

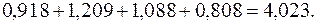
не равна четырем. Чтобы эта сумма равнялась четырем, умножим каждое слагаемое на поправочный коэффициент

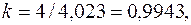
т.е.

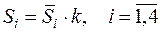(11)

Значения скорректированных сезонных компонент записаны в последней строке таблицы 6. Теперь их сумма равна четырем. Занесем эти значения в новую таблицу (колонка 3 таблицы 7):

Таблица 7.

t	yt	Si		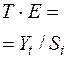T	T·S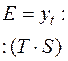
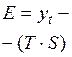
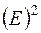
		0,913	78,86	87,80	80,16	0,898	-8,165	66,66
		1,202	83,19	85,03	102,20	0,978	-2,204	4,86
		1,082	83,18	82,25	89,00	1,011	1,002	1,00
		0,803	79,70	79,48	63,82	1,003	0,179	0,03
		0,913	76,67	76,70	70,03	1,000	-0,030	0,00
		1,202	76,54	73,93	88,86	1,035	3,139	9,85
		1,082	73,94	71,15	76,99	1,039	3,013	9,08
		0,803	72,23	68,38	54,91	1,056	3,093	9,57
		0,913	67,91	65,60	59,90	1,035	2,105	4,43
		1,202	66,56	62,83	75,52	1,059	4,482	20,08
		1,082	62,85	60,05	64,98	1,047	3,024	9,14
		0,803	59,78	57,28	45,99	1,044	2,007	4,03
		0,913	56,96	54,50	49,76	1,045	2,240	5,02
		1,202	49,92	51,73	62,18	0,965	-2,176	4,73
		1,082	46,21	48,95	52,97	0,944	-2,966	8,79
		0,803	37,36	46,18	37,08	0,809	-7,080	50,12

Шаг 3. Разделим каждый уровень исходного ряда на соответствующие значения сезонной компоненты. Тем самым мы получим величины

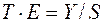, (12)

которые содержат только тенденцию и случайную компоненту (колонка 4).

Шаг 4. Определим трендовую компоненту в мультипликативной модели. Для этого рассчитаем параметры линейного тренда, используя уровни (Т+Е). Уравнение тренда имеет вид:

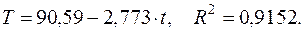
Подставляя в это уравнение значения 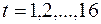, найдем уровни Т для каждого момента времени (колонка 5 таблицы).

Шаг 5. Найдем уровни ряда по мультипликативной модели, умножив уровни Т на значения сезонной компоненты для соответствующих кварталов (колонка 6 таблицы).

Шаг 6. Расчет ошибок в мультипликативной модели произведем по формуле:

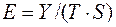. (13)

Численные значения ошибок приведены в колонке 7 таблицы. Для того, чтобы сравнить мультипликативную модель и другие модели временного ряда, можно по аналогии с аддитивной моделью использовать сумму квадратов абсолютных ошибок. Абсолютные ошибки в мультипликативной модели определяются как:

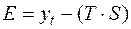(14)

В данной модели сумма квадратов абсолютных ошибок составляет 207,4. Общая сумма квадратов отклонений фактических уровней этого ряда от среднего значения равна 5023. Таким образом, доля объясненной дисперсии уровней ряда составляет 95,9%.

Прогнозирование по аддитивной или мультипликативной модели временного ряда сводится к расчету будущего значения временного ряда по уравнению модели без случайной составляющей в виде

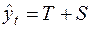(1’)

для аддитивной или

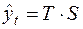(2’)

для мультипликативной модели.

Теперь рассмотрим модели временных рядов, где в качестве исходных статистических данных мы располагаем наблюдениями двух временных рядов 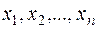и 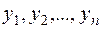. Целью регрессионного анализа в данном случае является построение линейной регрессионной модели, позволяющей с наименьшими ошибками прогнозировать значения y_t по значениям x_t для t>n.

Подобные модели естественны в ситуациях, когда две переменные x и y связаны так, что воздействия единовременного изменения одной из них (x) на другую (y) сказывается в течение достаточно продолжительного времени, т.е. наблюдается распределенный во времени эффект воздействия. В частности, такие связи возникают между регистрируемыми во времени входными и выходными характеристиками процессов накопления и распределения ресурсов (например, процессов преобразования доходов населения в его расходы) или процессов трансформации затрат в результаты (например, процессов воспроизводства основных доходов).

Эконометрическая модель является динамической, если в данный момент t она учитывает значения входящих в неё переменных, относящихся как к текущему, так и к предыдущим моментам времени, т.е. модель учитывает, отражает динамику исследуемых переменных в каждый момент времени.

Переменные, влияние которых характеризуется определенным запаздыванием, называются лаговыми переменными.

Классифицируются динамические модели по – разному. Один из вариантов классификации следующий:

1. Модели с распределенными лагами. Они содержат в качестве лаговых переменных лишь независимые (объясняющие) переменные, например:

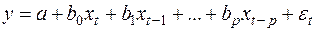(15)

2. Авторегрессионные модели, уравнения которых включают в качестве объясняющих переменных лаговые значения зависимых переменных, например:

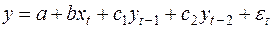(16)

Рассмотрим модель (15), приняв, что р – конечное число. Модель говорит о том, что если в некоторый момент времени t происходит изменение х, это изменение будет влиять назначение у в течение р последующих моментов времени. Коэффициент b₀ называется краткосрочным мультипликатором, т.к. он характеризует изменение среднего значения у при единичном изменении х в тот же самый момент времени. Сумма 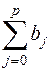называется долгосрочным мультипликатором; он характеризует изменение у под воздействием единичного изменения х в каждом из моментов времени. Любая сумма 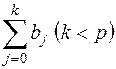называется промежуточным мультипликатором.

Относительные коэффициенты модели (15) с распределенным лагом определяются выражениями:

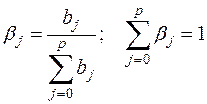(17)

(условие нормировки имеет место, только если все b_j имеют одинаковые знаки). Значения β_j являются весами для соответствующих коэффициентов b_j. Каждый из них измеряет долю общего изменения у, приходящегося на момент (t+j).

Средний лаг определяется по формуле средней арифметической взвешенной:

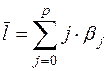(18)

Он означает период, в течение которого происходит изменение результата от изменения х в момент t. Небольшая величина (18) означает быструю реакцию у на изменение х, высокое значение говорит о том, что воздействие фактора у будет сказываться в течение длительного времени.

Медианный лаг – это величина лага, для которого

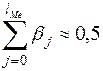(19)

Это время, в течение которого с момента t будет реализована половина общего воздействия фактора на результат.

Рассмотрим условный пример. Предположим, модель зависимости объёмов продаж компании от расходов на рекламу имеет вид:

.

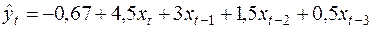Краткосрочный мультипликатор равен 4,5: увеличение расходов на рекламу на 1 млн. руб. приводит к среднему росту продаж компании на 4,5 млн. руб. в том же периоде.

В момент (t+1) такой рост составит 4,5+3,0=7,5 млн. руб., в момент (t+2) - 7,5+1,5=9 млн. руб. и т.д. долгосрочный мультипликатор равен 9,5. В долгосрочной перспективе (в течение 3 месяцев) увеличение расходов на 1 млн. руб. приведет к общему росту продаж на 9,5 млн. руб.

Относительные коэффициенты:

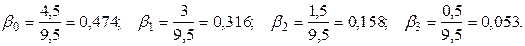
47,4% общего увеличения объёма продаж от роста затрат на рекламу происходит в текущем месяце, 31,6% - в следующем месяце и т.д.

Средний лаг равен:

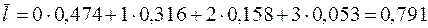(мес.)

- небольшая величина, поскольку большая часть эффекта роста затрат на рекламу проявляется сразу же. Медианный лаг в данном примере составляет чуть более 1 месяца.

Модель (15) можно свести к уравнению множественной регрессии через замены переменных:

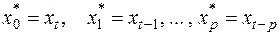, (20)

в результате получаем:

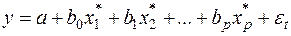(21)

Однако применение обычного МНК затруднительно по следующим причинам:

1. Текущие и лаговые значения х тесно связаны между собой, что приводит к высокой мультиколлинеарности факторов.

2. При большой величине лага велико число параметров, что приводит к уменьшению числа степеней свободы.

3. Часто возникает проблема автокорреляции остатков.

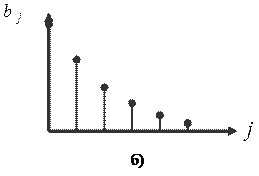
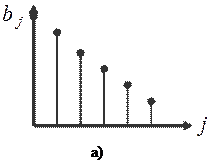
Поэтому оценки параметров становятся неточными и неэффективными. Для получения более обоснованных оценок нужна информация о структуре лага. Эта структура может быть различной. На рисунке представлены некоторые её формы:

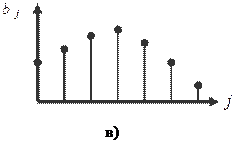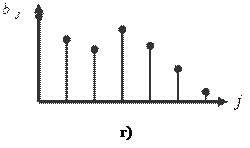Если с ростом величины лага коэффициенты при лаговых переменных убывают, то имеет место линейная (или треугольная) структура лага (а), а также геометрическая структура (б). Возможны и другие структуры лага (в или г). Рассмотрим некоторые подходы к расчету лагов.

Лаги Алмон. Предполагается, что в модели (15) с конечной максимальной величиной лага р значения коэффициентов b_j описываются полиномом к – й степени:

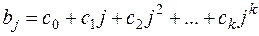(22)

Каждый коэффициент, таким образом, запишется так:

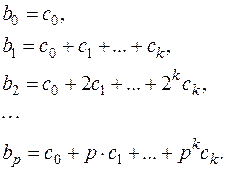(23)

Подставим эти соотношения в (15) и перегруппируем слагаемые, получим:

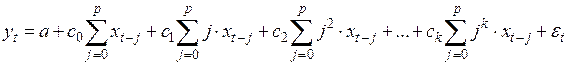(24)

Обозначим суммы соответственно как новые переменные 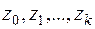, перепишем (24) в виде:

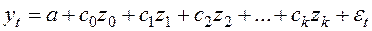(25)

Параметры с_j определяются по МНК.

Достоинства метода:

1. Универсальность, применимость для моделирования процессов с разнообразными структурами лагов.

2. При малых k (2 или 3) можно построить модели с распределенным лагом любой длины.

Ограничения метода:

1. Величина р должна быть известна заранее. При этом приходится задавать максимально возможную величину лага. Выбор меньшего лага, чем его реальное значение, приведет к неверной спецификации модели, невозможности обеспечить случайность остатков, поскольку влияние значимых факторов будет выражено в остатках. Оценки параметров при этом окажутся неэффективными и смещенными. Включение в модель большей величины лага, чем его реальное значение, снижает эффективность оценок из – за наличия статистически незначимых факторов.

2. Необходимость установить степень полинома. Обычно принимают k =2 или 3 по правилу: степень полинома k должна быть на единицу больше числа экстремумов в структуре лага. В крайнем случае k определяется из сравнения моделей для различных k.

3. Возможна мультиколлинеарность факторов z_j, однако она сказывается здесь в меньшей степени, чем в модели (15).

Метод Койка. Этот метод применяется в модели с бесконечным лагом:

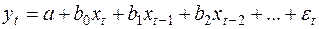(26)

Здесь обычный МНК применить нельзя. Для идентификации модели (26) предполагается, что параметры с увеличением лага убывают в геометрической прогрессии, т.е. с постоянным темпом :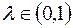

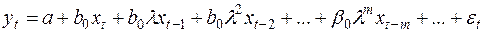(27)

Запишем выражение (27) для момента (t-1):

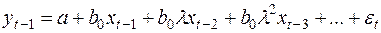(28)

Умножим (28) на λ и вычтем из (27):

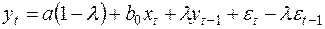
или

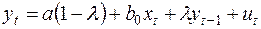(29)

Это модель авторегрессии. Определив её параметры, находим λ, а, b₀ исходной модели, а затем и параметры 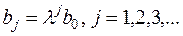. Данная модель позволяет определить долгосрочный мультипликатор 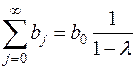и средний лаг .

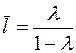Теперь перейдем к рассмотрению авторегрессионных моделей.

Модель адаптивных ожиданий. Моделирование ожиданий является сложной задачей, поскольку фактор ожидания имеет качественную специфику. Например, инвестиции связаны не только с нормой процента, но и с ожиданиями инвесторов. Если в стране существенная безработица, то действия правительства в направлении стимулирования могут рассматриваться как позитивные, и это способствует инвестициям. Если экономика близка к полной занятости, то та же самая политика будет рассматриваться как ведущая к росту инфляции и приведет к падению инвестиционной активности.

Модель адаптивных ожиданий заключается в простой процедуре корректировки ожиданий, когда в каждый момент времени реальное значение переменной сравнивается с её ожидаемым значением. Если реальное значение оказывается больше, то ожидаемое в следующий момент значение корректируется в сторону его увеличения, если меньше – то в сторону уменьшения. Предполагается, что размер корректировки пропорционален разности между реальным и ожидаемым значениями переменной. Таким образом, основную идею можно записать формулой:

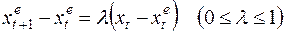(30)

где 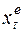- значение х, ожидаемое в момент t (expected). Это выражение можно переписать в форме взвешенного среднего:

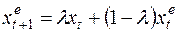(31)

Модель (30) и является моделью адаптивных ожиданий. Это выражение иногда называют моделью обучения на ошибках, т.к. ожидания экономических объектов складываются из прошлых ожиданий, поправленных на величину ошибки в ожиданиях, допущенных ранее.

При λ =0 ожидания являются статичными, неизменными, т.е. .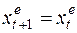

При λ =1 ожидания реализуются мгновенно, т.е. .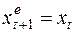

Чем больше λ, тем быстрее ожидаемое значение адаптируется к предыдущим реальным значениям переменной.

Долгосрочная функция модели адаптивных ожиданий записывается в виде:

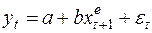(32)

Подставим сюда выражение (31), получим:

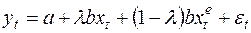(33)

Запишем его для (t-1):

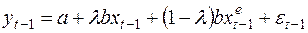(34)

Умножим (34) на (1-λ) и вычтем почленно из (32):

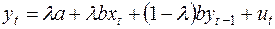, (35)

где .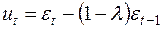

Это модель авторегрессии, в которой все переменные имеют фактические, а не ожидаемые значения. Модель в форме (35) называется краткосрочной функцией модели адаптивных ожиданий.

Модель неполной (частичной) корректировки. Здесь пове-денческое уравнение определяет не фактическое значение y_t, а её желаемый (целевой) уровень :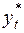

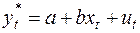(36)

Примером такой модели служит политика компаний относительно распределения дивидендов: прибыль расходуется частично на уплату дивидендов, частью на инвестиции. Когда прибыль увеличивается, дивиденды тоже растут, но не в той же пропорции (это объясняется желанием руководства фирмы в любом случае не уменьшать дивиденды, т.к. это ударяет по репутации фирмы).

В модели предполагается, что фактическое приращение зависимой переменной пропорционально разнице между её желаемым уровнем и значением в предыдущий период:

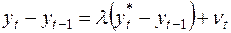(37)

(ν_t – случайный член). Это выражение можно переписать так:

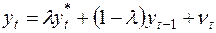, (38)

т.е. в форме взвешенного среднего. Чем больше λ, тем быстрее идет корректировка. При λ =1 полная корректировка происходит за один период. При λ =0 корректировка не происходит совсем.

Подставим (36) в (38), получим:

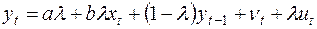(39)

Это и есть модель частичной корректировки, которая также является моделью авторегрессии.

Несколько слов об оценке параметров уравнений авторегрессии. Рассмотрим уравнение:

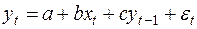(40)

Во всех рассмотренных выше моделях стоит проблема оценивания параметров. Обычный МНК чаще всего даёт смещенные и несостоятельные оценки, вследствие автокорреляции между случайными отклонениями ε_t и ε_t-1 и корреляции между y_t-1 и ε_t.

Один из возможных методов расчета параметров – метод инструментальных переменных, состоящий в замене y_t-1 на новую переменную, которая тесно коррелирует с y_t-1, но не коррелирует с остатками. Это можно сделать двумя способами.

1. Провести регрессию

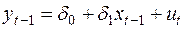, (41)

или

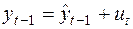
и подставить 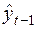в уравнение авторегрессии, получаем:

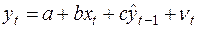, (42)

и далее применяем обычный МНК.

2. Подставим (41) в (40), получим модель с распределенным лагом:

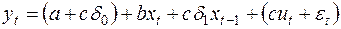, (43)

для которой не нарушаются предпосылки обычного МНК.

Список учебной литературы

1. Эконометрика: Учебник /Под ред. И.И. Елисеевой/ - М.: Финансы и статистика, 2001. – 344с.

2. Практикум по эконометрике: Учебное пособие / И.И. Елисеева и др./ - М.: Финансы и статистика, 2001. – 192с.

3. Бородич С.А. Эконометрика: Учебное пособие. – М.: Новое издание. 2001. – 408с.

4. Магнус Я.Р., Катышев П.К., Пересецкий А.А., Эконометрика. Начальный курс. Учебное пособие. – М.: Дело, 1998. – 248с.

5. Доугерти К. Введение в эконометрику. – М.: ИНФРА-М, 1997. – 402с.

6. Колемаев В.А., Калинина В.Н. Теория вероятностей и математическая статистика. – М.: ЮНИТИ, 2003. – 352с.

7. Айвазян С.А., Мхитарян В.С. Теория вероятностей и прикладная статистика – М.: ЮНИТИ - ДАНА, 2001. – 656с.

8. Айвазян С.А. Основы эконометрики. – М.: ЮНИТИ - ДАНА, 2001. –432с.

Дата добавления: 2013-12-11