Деформация стержня

Упругая деформация пружины.

При растяжении пружины (рис 2.14) на величину 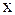относительно её равновесного состояния (х₀ = 0) возникает упругая сила 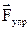, которая возвращает пружину в прежнее положение после прекращения действия внешней силы. Модуль упругой силы, возникающей прилинейном растяжении или сжатии пружины определяется законом Гука.

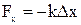, (2.56)

где 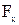– проекция силы упругости на ось x, знак минус учитывает противоположные направления силы 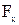и перемещения пружины .

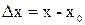Стержень длинной l₀ и сечением S при действии сил 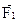и 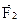перпендикулярно его торцам в противоположных направлениях деформируется (растягивается или сжимается) (рис 2.15). Деформация стержня определяется относительной величиной

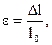(2.57)

где ∆ l = l - l₀, l- длинна стержня после деформации.

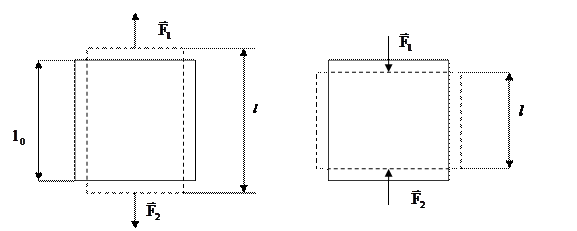
Рис. 2.15

Опыт показывает, что

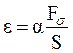, (2.58)

где α – коэффициент упругости стержня,

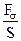=σ – нормальное напряжение, измеряемое в 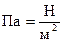(паскаль).

Наряду с коэффициентом упругости a для характеристики упругих свойств тел при нормальных напряжениях используют модуль Юнга Е = 1/a, который, как и напряжение, измеряется в паскалях.

Относительное удлинение (сжатие) и модуль Юнга в соответствии с равенствами (2.13 и 2.14) определяется из соотношений:

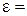
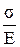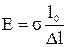, . (2.59)

Модуль Юнга равен такому нормальному напряжению, при котором деформация стержня Dl равна его первоначальной длине l₀. В действительности при таких напряжениях происходит разрушение стержня.

Решая уравнение (2.58) относительно F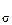, и подставляя вместо e = Dl/l₀, a = 1/Е, получим формулу для определения силы деформирующей стержень с сечением S на величину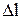

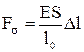, (2.60)

где 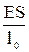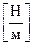– постоянный для стержня коэффициент, который в соответствии с законом Гука соответствует коэффициенту упругости стержня при его сжатии и растяжении.

При действии на стержень касательного (тангенциального) напряжения

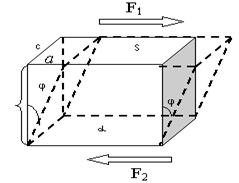
силы F₁ и F₂ приложены параллельно противоположным граням площадью S прямоугольного стержня вызывают деформацию сдвига (рис 2.16).

b

Рис. 2.16

Если действие сил равномерно распределено по всей поверхности соответствующей грани, то в любом сечении, параллельном этим граням, возникает тангенциальное напряжение 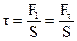. Под действием напряжений тело деформируется так, что одна грань сместиться относительно другой на некоторое расстояние а. Если тело мысленно разбить на элементарные, параллельные рассматриваем граням слои, то каждый слой окажется сдвинутым относительно соседних с ним слоев.

При деформации сдвига любая прямая, первоначально перпендикулярная к слоям, отклонится на некоторый угол φ. тангенс которого называется относительным сдвигом

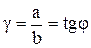, (2.61)

где b – высота грани. При упругих деформациях угол φ очень мал, поэтому можно считать, что 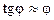и .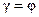

Опыт показывает, что относительный сдвиг пропорционален тангенциальному напряжению

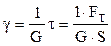, (2.62)

где G – модуль сдвига.

Модуль сдвига 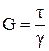зависит только от свойств материала и равен тангенциальному напряжению при угле φ = 45˚. Модуль сдвига так же, как и модуль Юнга измеряется в паскалях (Па). Сдвиг стержня на угол 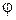вызывает сила

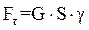=G S φ, (2.63)

где G·S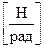– коэффициент упругости стержня при деформации сдвига.

Дата добавления: 2013-12-11