Определение минимального количества измерений

Внутрисерийная дисперсия σ2 вс характеризует случайные погрешности измерений, так как только случайные влияния обусловливают те различия (отклонения результатов наблюдений), на которых она основана. В то же время рассеяние хj *, различных серий обусловливается не только случайными погрешностями измерений, но и систематическими различиями (если они существуют) между результатами наблюдений, сгруппированными по сериям. Следовательно, усредненная межсерийная дисперсия

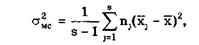
где 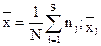выражает силу действия фактора, вызывающего систематические различия между сериями.

Таким образом, σ_вс²/(σ_вс² + σ_мс²) характеризует долю дисперсии всех результатов наблюдений, обусловленную наличием случайных погрешностей измерений, а σ_мс²/(σ_вс² + σ_мс²) — долю дисперсии, обусловленную межсерийными различиями результатов наблюдений. Первую из них называют коэффициентом ошибки, вторую — показателем дифференциации. Чем больше отношение показателя дифференциации к коэффициенту ошибки, тем сильнее действие фактора, по которому группировались серии, и тем больше систематическое различие между ними.

Критерием оценки наличия систематических погрешностей в данном случае является дисперсионный критерий Фишера F = σ_мс²/σ_вс². Критическая область для критерия Фишера соответствует P(F > Fq) = q.

Значения Fq для различных уровней значимости q, числа измерений N и числа серий s приведены в приложении 1, где k₂ = N-s, k₁= s — 1. Если полученное значение критерия Фишера больше F_q (при заданных q, N и s), то гипотеза об отсутствии систематических смещений результатов наблюдений по сериям отвергается, т.е. обнаруживается систематическая погрешность, вызываемая тем фактором, по которому группировались результаты наблюдений.

Пример 5.4. Было сделано 38 измерений диаметра детали восемью различными штангенциркулями. Каждым из них проводились по пять измерений. Внутрисерийная дисперсия равна 0,054 мм2, межсерийная — 0,2052 мм2. Определить наличие систематической погрешности измерения диаметра детали. Расчетное значение критерия Фишера F = 0,2052/0,054 = 3,8. Для s-1 = 7, N-s = 30 по таблице значений критерия Фишера имеем при q = 0,05 F_0,05 = 2,3 и при q = 0,01 F_0,01 = 3,3. Полученное значение F больше, чем 2,3 и 3,3. Следовательно, в результатах наблюдений обнаруживается наличие систематических погрешностей.

Из всех рассмотренных способов обнаружения систематических погрешностей дисперсионный анализ является наиболее эффективным и достоверным, так как позволяет не только установить факт наличия погрешности, но и дает возможность проанализировать источники ее возникновения.

Критерий Вилкоксона. Если закон распределения результатов измерений неизвестен, то для обнаружения систематической погрешности применяют статистический критерий Вилкоксона.

Из двух групп результатов измерений х₁, х₂,..., х_n и у₁ у₂,…, у_m, где n ≥ m ≥ 5, составляется вариационный ряд, в котором все n + m значений х₁, х₂,..., х_n; у₁, у₂,...,y_m располагают в порядке их возрастания и приписывают им ранги — порядковые номера членов вариационного ряда. Различие средних значений каждого из рядов можно считать допустимым, если выполняется неравенство

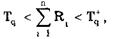
где R₁ — ранг (номер) члена х_i, равный его номеру в вариационном ряду; Т_q^- и T_q⁺—нижнее и верхнее критические значения для выбранного уровня значимости q. При m < 15 эти критические значения определяются по табл. 5.3. При m >15 они рассчитываются по формулам:

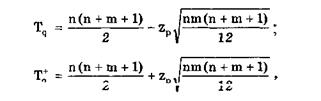
где z_p— квантиль нормированной функции Лапласа.

Более полная таблица значений критических значений Т_q^- и Т_q⁺ приведена в рекомендации МИ 2091-90 ГСИ. Измерения физических величин. Общие требования".

Исключение систематических погрешностей путем введения поправок. В ряде случаев систематические погрешности могут быть вычислены и исключены из результата измерения. Для этого используются поправки. Поправка С_j — величина, одноименная измеряемой, которая

Таблица5.3

Критические значения Т_q^- и Т_q⁺ при q = 0,05 и 0,01.

n	m	q = 0,05	q = 0,01
Tq^-	Tq^+	Tq^-	Tq^+

вводится в результат измерения х_i = x_i^` + Q_j + С_j с целью исключения составляющих систематической погрешности Q_j. При С_J = - Q_j j-я составляющая систематической погрешности полностью устраняется из результата измерения. Поправки определяются экспериментально или в результате специальных теоретических исследований. Они задаются в виде таблиц, графиков или формул.

Введением одной поправки устраняется влияние только одной составляющей систематической погрешности. Для устранения всех составляющих в результат измерения приходится вводить множество поправок. При этом вследствие ограниченной точности определения поправок случайные погрешности результата измерения накапливаются и его дисперсия увеличивается. Так как поправка известна с определенной точностью, то она характеризуется статистически — средним значением поправки С и СКО S_c. При исправлении результата х_i^` путем введения поправок С_j где j = l, 2,..., m, по формуле

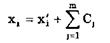
дисперсия исправленного результата

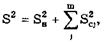
где S_н² — оценка дисперсии неисправленного результата; S_cj² —оценка дисперсии j-й поправки. Как видно, с одной стороны, уточняется результат измерения, а с другой — увеличивается разброс за счет роста дисперсии. Следовательно, необходимо найти оптимум.

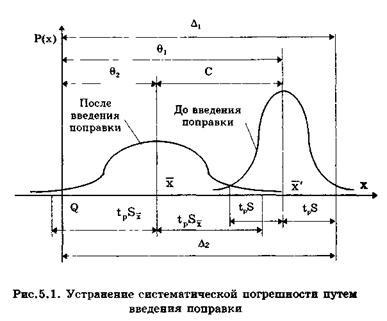Пусть при измерении постоянной величины Q получено (рис.5.1) значение Q = х*' ± t_pS, где х*'— оценка среднего арифметического неисправленного результата измерений; t_p — коэффициент Стьюдента.

После введения поправки С ± t_pS_c результат измерения

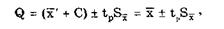
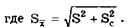
Максимальные доверительные значения погрешности результата измерения до и после введения поправки равны соответственно

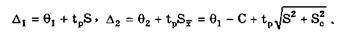
Поправку имеет смысл вводить до тех пор, пока Δ₁ < Δ₂. Отсюда следует, что

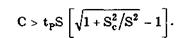
Если S_с/S << 1, то, раскладывая уравнение в степенной ряд, получим С > 0,5 S²_c / S². Из этого неравенства видно, что если оценка среднего квадратического отклонения поправки Sc → 0, то поправку имеет смысл вводить всегда.

В практических расчетах погрешность результата обычно выражается не более чем двумя значащими цифрами, поэтому поправка, если она меньше пяти единиц младшего разряда, следующего за последним десятичным разрядом погрешности результата, все равно будет потеряна при округлении и вводить ее не имеет смысла.

Пример. Напряжение источника ЭДС Ux с внутренним сопротивлением R_i = 60±10 Ом измерено вольтметром класса точности 0,5. Сопротивление вольтметра Rv = 5 кОм и известно с погрешностью +0,5%. Показание вольтметра Uv = 12,35 В. Найти поправку, которую нужно внести в показание прибора для определения действительного значения напряжения источника ЭДС.

Показания вольтметра соответствуют падению напряжения на нем:

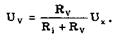
Относительная систематическая методическая погрешность, обусловленная ограниченным значением сопротивления Rv,

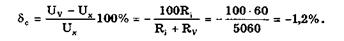
Поправка равна абсолютной погрешности, взятой с обратным знаком: Δс= 0,012·12,35 = 0,146 В. Погрешность полученного значения поправки определяется погрешностью, с которой известно сопротивление R_i. Ее предельное значение составит 10/60 = 0,167. Погрешностью из-за неточности оценки Rv, равной 0,005, можно пренебречь. Следовательно, погрешность определения поправки Δ = ±0,167-0,146 ≈ 0,03 В.

Таким образом, поправка, которую необходимо ввести в показания вольтметра с учетом округления ΔU = +0,15 В. Тогда исправленное значение U'x = 12,35+0,15 = 12,50 В. Этот результат имеет определенную погрешность, в том числе неисключенный остаток систематической погрешности Δ = ± 0,03 В или δ = + 0,24% из-за потребления некоторой

мощности вольтметром.

Суммирование систематических погрешностей. Независимо от того, к какому виду относится измерение, является ли оно прямым, косвенным, совместным или совокупным, систематическая погрешность результата измерения оценивается, как правило, по ее известным составляющим. Поскольку в каждом конкретном случае каждая систематическая состав­ляющая получает конкретную реализацию (она либо постоянная, либо известен закон ее изменения), то результирующая, суммарная система­тическая погрешность представляет собой алгебраическую сумму со­ставляющих.

6. Обработка результатов экспериментальных исследований

6.1 Основы теории случайных ошибок и методов оценки случайных погрешностей в измерениях

Анализ случайных погрешностей основывается на тео­рии случайных ошибок, дающей возможность с опреде­ленной гарантией вычислить действительное значение измеренной величины и оценить возможные ошибки.

Основу теории случайных ошибок составляют пред­положения о том, что при большом числе измерений слу­чайные погрешности одинаковой величины, но разного знака встречаются одинаково часто; большие погрешно­сти встречаются реже, чем малые (вероятность появления погрешности уменьшается с ростом ее величины); при бесконечно большом числе измерений истинное зна­чение измеряемой величины равно среднеарифметичес­кому значению всех результатов измерений, а появление того или иного результата измерения как случайного со­бытия описывается нормальным законом распределения.

Различают генеральную и выборочную совокупность измерений. Под генеральной совокупностью подразуме­вают все множество возможных значений измерений x_iили возможных значений погрешностей Δx_i. Для выбо­рочной совокупности число измерений n ограничено, и в каждом конкретном случае строго определяется. Обычно считают, если n > 30, то среднее значение дан­ной совокупности измерений хдостаточно приближается к его истинному значению.

Теория случайных ошибок позволяет оценить точ­ность и надежность измерения при данном количестве замеров или определить минимальное количество заме­ров, гарантирующее требуемую (заданную) точность и надежность измерений. Наряду с этим возникает необходимость исключить грубые ошибки ряда, определить достоверность полученных данных и др.

Интервальная оценка с помощью доверительной веро­ятности. Для большой выборки и нормального закона распределения общей оценочной характеристикой изме­рения являются дисперсия Dи коэффициент вариа­ции k_B:

D = σ² = Σ(x_i –x)² / (n-1); k_B = σ/x. (1)

Дисперсия характеризует однородность измерения. Чем выше D,тем больше разброс измерений. Коэффици­ент вариации характеризует изменчивость. Чем выше k_B, тем больше изменчивость измерений относительно сред­них значений, k_Bоценивает также разброс при оценке нескольких выборок.

Доверительным называется интервал значений x_i,в который попадает истинное значение х_дизмеряемой величины с заданной вероятностью. Доверительной ве­роятностью (достоверностью) измерения называется вероятность того, что истинное значение измеряемой ве­личины попадает в данный доверительный интервал, т. е. в зону a ≤ x_д ≤ b. Эта величина определяется в долях еди­ницы или в процентах. Доверительная вероятность р_д описывается выражением

Р_д = р[а ≤ х_д ≤ b] = (1/2) [φ (b - х)/σ - φ(а - х)/ σ],

где φ(t) - интегральная функция Лапласа (табл. 1), определяемая выражением

φ(t) = .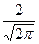

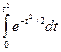Аргументом этой функции является отношение µ к сред­неквадратичному отклонению σ,т.е.

t =µ/σ, (2)

где t - гарантийный коэффициент;

µ = b - х, µ = а - х.

Если же на основе определенных данных установлена доверительная вероятность р_д (часто ее принимают рав­ной 0,90; 0,95; 0,9973), то устанавливается точность из­мерений (доверительный интервал 2µ)на основе соот­ношения р_д = φ(µ/σ). Половина доверительного интерва­ла равна

µ= σ arg φ(р_д) = σt, (3)

где arg φ(р_д) - аргумент функции Лапласа, а при n < 30 — функции Стьюдента (табл. 2). Доверительный интервал характеризует точность измерения данной вы­борки, а доверительная вероятность - достоверность из­мерения. Пусть, например, выполнено 30 измерений проч­ности покрытия участка автомобильной дороги при среднем модуле упругости покрытия Е=170 МПа и вычисленном значении среднеквадратического откло­нения σ = 3,1 МПа.

Таблица 1. Интегральная функция Лапласа

t	pд	t	pд	t	pд
0,00	0,0000	0,75	0,5467	1,50	0,8664
0,05	0,0399	0,80	0,5763	1,55	0,8789
0,10	0,0797	0,85	0,6047	1,60	0,8904
0,15	0,1192	0,90	0,6319	1,65	0,9011
0,20	0,1585	0,95	0,6579	1,70	0,9109
0,25	0,1974	1,00	0,6827	1,75	0,9199
0,30	0,2357	1,05	0,7063	1,80	0,9281
0,35	0,2737	1,10	0,7287	1,85	0,9357
0,40	0,3108	1,15	0,7419	1,90	0,9426
0,45	0,3473	1,20	0,7699	1,95	O.P488
0,50	0,3829	1,25	0,7887	2,00	0,9545
0,55	0,4177	1,30	0,8064	2,25	0,9756
0,60	0,4515	1,35	0,8230	2,50	0,9876
0,65	0,4843	1,40	0,8385	3,00	0,9973
0,70	0,5161	1,45	0,8529	4,00	0,9999

Требуемую точность измерений можно определить для разных уровней доверительной вероятности (р_д = 0,9; 0,95; 0,9973), приняв значения tпо табл.1. В этом случае соответственно µ = ±3,1 · 1,65 = 5,1; ±3,1 · 2,0 = 6,2; ±3,1 · 3,0 = 9,3 МПа. Следовательно, для данного сред­ства и метода доверительный интервал возрастает при­мерно в два раза, если увеличить р_д только на 10%.

Если необходимо определить достоверность измерений для установленного доверительного интервала, напри­мер µ = ±7 МПа, то по формуле t =µ/σ = 7/3,1 = = 2,26. По табл.1 для t =2,26 определяем р_д=0,97. Это означает, что в заданный доверительный интервал из 100 измерений не попадают только три.

Значение (1 - р_д) называют уровнем значимости. Из него следует, что при нормальном законе распреде­ления погрешность, превышающая доверительный интер­вал, будет встречаться один раз из n_и измерений, где

n_{и =} р_д /(1 – р_д) (4)

или иначе приходится браковать одно изn_иизмерений.

По данным приведенного выше примера можно вы­числить количество измерений, из которых одно изме­рение превышает доверительный интервал. По формуле (4) при р_д = 0,9; определяется n_и = 0,9/(1 - 0,9) = 9 из­мерений. При р_д, равной 0,95 и 0,9973, соответственно 19 и 367 измерениий

Для проведения опытов с заданной точностью и досто­верностью необходимо знать то количество измерений, при котором экспериментатор уверен в положитель­ном исходе. В связи с этим одной из первоочередных задач при статических методах оценки является установление минимального, но достаточного числа изме­рений для данных условий. Задача сводится к уста­новлению минимального объема выборки (числа изме­рений) N_min при заданных значениях доверительного интервала 2µ и доверительной вероятности. При выпол­нении измерений необходимо знать их точность:

Δ = σ₀/x (5)

где σ_о - среднеарифметическое значение среднеквадра­тичного отклонения σ, равное σ_о = σ/.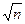

Таблица 2. Коэффициент Стьюдента α_ст.

n	Рд
0,80	0,90	0,95	0,99	0,995	0,999
	3,080	6,31	12,71	63,70	127,30	637,20
	1,886	2,92	4,30	9,92	14,10	31,60
	1,638	2,35	3,188	5,84	7,50	12,94
	1,533	2,13	2,77	4,60	5,60	8,61
	1,476	2,02	2,57	4,03	4,77	6,86
	1,440	1,94	2,45	3,71	4,32	9,96
	1,415	1,90	2,36	3,50	4,03	5,40
	1,397	1,86	2,31	3,36	3,83	5,04
	1,383	1,83	2,26	3,25	3,69	4,78
	1,363	1,80	2,20	3,11	3,50	4,49
	1,350	1,77	2,16	3,01	3,37	4,22
	1,341	1,75	2,13	2,95	3,29	4,07
	1,333	1,74	2,11	2,90	3,22	3,96
	1,328	1,73	2,09	2,86	3,17	3,88
	1,316	1,70	2,04	2,75	3,20	3,65
	1,306	1,68	2,02	2,70	3,12	3,55
	1,298	1,68	2,01	2,68	3,09	3,50
	1,290	1,67	2,00	2,66	3,06	3,46
∞	1,282	1,64	1,96	2,58	2,81	3,29

Значение σ_о часто называют средней ошибкой.Дове­рительный интервал ошибки измерения Δ определяется аналогично для измерений µ = tσ_о. С помощью tлегко определить доверительную вероятность ошибки измере­ний из табл.1.

В исследованиях часто по заданной точности Δ и до­верительной вероятности измерения определяют мини­мальное количество измерений, гарантирующих требуе­мые значения Δ и p_д.

Аналогично уравнению (3) с учетом (5) можно получить

µ = σarg φ (р_д) = σ_о/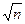t(6)

При N_min = n получаем

N_min = σ²t²/σ²_o = k²_в t²/Δ²,(7)

здесь k_в— коэффициент вариации (изменчивости), %; Δ - точность измерений, %.

Для определения N_minможет быть принята такая по­следовательность вычислений: 1) проводится предвари­тельный эксперимент с количеством измерений n,кото­рое составляет в зависимости от трудоемкости опыта от 20 до 50; 2) вычисляется среднеквадратичное отклоне­ние по формуле (1); 3) в соответствии с поставлен­ными задачами эксперимента устанавливается требуе­мая точность измерений Δ, которая не должна превышать точности прибора; 4) устанавливается нор­мированное отклонение t,значение которого обычно за­дается (зависит также от точности метода); 5) по фор­муле (7) определяют N_minи тогда в дальнейшем в процессе эксперимента число измерений не должно быть меньше N_min.

Пусть, например, при приемке сооружений комиссия в качестве одного из параметров замеряет их ширину. Согласно инструкции требуется выполнять 25 измере­ний; допускаемое отклонение параметра ±0,1 м. Если предварительно вычисленное значение σ = 0,4м, то мож­но определить, с какой достоверностью комиссия оцени­вает данный параметр. Согласно инструкции Δ = 0,1 м. Изформулы (7) можно записать t = 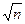Δ/σ = 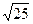·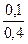=1.25. В соответствии с табл. 1 доверительная вероятность для t = 1,25р_д = 0,79 это низкая ве­роятность. Погрешность, превышающая доверительный ин­тервал 2µ = 0,2 м, согласно выражению (4) будет встре­чаться один раз из 0,79/(1 - 0,79) = 3,37, т. е. из четырех измерений. Это недопустимо. В связи с этим необходимо вы­числить минимальное количе­ство измерений с доверитель­ной вероятностью р_д,равной 0,9 и 0,95. По формуле (7) имеем N_min = 0,4² - 1,65/0,1² = 43 измерения при р_д = 0,90 и 64 измерения при р_д = 0,95, что значительно превышает ус­тановленные 25 измерений.

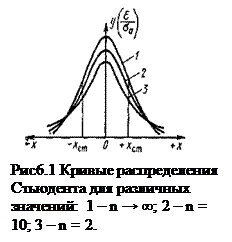
Оценки измерений с помощью σ и σ_о по приведенным методам справедливы при n > 30. Для нахождения гра­ницы доверительного интервала при малых значениях применяют метод, предложенный в 1908 г. английским математиком В. С. Госсетом (псевдоним Стьюдент). Кривые распределения Стьюдента в случае n → ∞ (прак­тически при n > 20) переходят в кривые нормального рас­пределения (рис. 1).

Для малой выборки доверительный интервал

µ_ст = σ_о α_ст, (8)

где α_ст - коэффициент Стьюдента, принимаемый по табл. 2 в зависимости от значения доверительной ве­роятности р_д.

Зная µ_ст, можно вычислить действительное значение изучаемой величины для малой выборки

х_д = х ± µ_ст (9)

Возможна и иная постановка задачи. По n известных измерений малой выборки необходимо определить довери­тельную вероятность р_д при условии, что погрешность среднего значения не выйдет за пределы ± µ_ст. Задачу решают в такой последовательности: вначале вычисляется среднее значение х, σ_о и α_ст = µ_ст/σ_о. С помощью величины α_ст, известного n и табл. 2 определяют до­верительную вероятность.

Дата добавления: 2013-12-11