Определение. Выражение называется формулой

Функция f(x) = ln(1 + x).

Рис. 3. Шесть членов разложения

Рис. 2. Четыре члена разложения

Рис. 1. Два члена разложения

Функция f(x) = (1 + x)a.

Функция f(x) = cosx.

Функция f(x) = sinx.

Функция f(x) = ex.

Находим: f(x) = e^x, f(0) = 1

f¢(x) = e^x, f¢(0) = 1

……………………

f⁽ⁿ⁾(x) = e^x, f⁽ⁿ⁾(0) = 1

Тогда: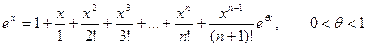

Пример: Найдем значение числа е.

В полученной выше формуле положим х = 1.

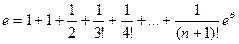
Для 8 членов разложения: e = 2,71827876984127003

Для 10 членов разложения: e = 2,71828180114638451

Для 100 членов разложения: e = 2,71828182845904553

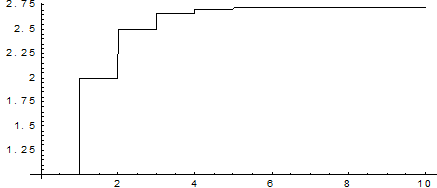
На графике показаны значения числа е с точностью в зависимости от числа членов разложения в ряд Тейлора.

Как видно, для достижения точности, достаточной для решения большинства практических задач, можно ограничиться 6-7 – ю членами ряда.

Получаем f(x) = sinx; f(0) = 0

f¢(x) = cosx = sin(x + p/2); f¢(0) = 1;

f¢¢(x) = -sinx = sin(x + 2p/2); f¢¢(0) = 0;

f¢¢¢(x) = -cosx = sin(x + 3p/2); f¢¢¢(0)=-1;

…………………………………………

f⁽ⁿ⁾(x) = sin(x + pn/2); f⁽ⁿ⁾(0) = sin(pn/2);

f⁽ⁿ⁺¹⁾(x) = sin(x + (n + 1)p/2); f⁽ⁿ⁺¹⁾(e) = sin(e + (n + 1)p/2);

Итого: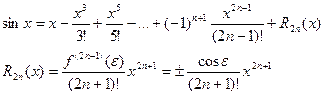

Для функции cosx, применив аналогичные преобразования, получим:

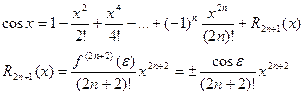
(a - действительное число)

…………………………………………………..

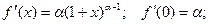
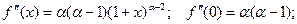
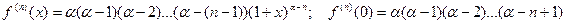
Тогда:

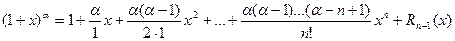
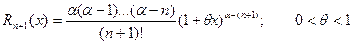
Если в полученной формуле принять a = n, где n- натуральное число и f⁽ⁿ⁺¹⁾(x)=0, то R_n+1 = 0, тогда

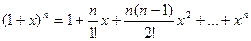
Получилась формула, известная как бином Ньютона.

Пример: Применить полученную формулу для нахождения синуса любого угла с любой степенью точности.

На приведенных ниже графиках представлено сравнение точного значения функции и значения разложения в ряд Тейлора при различном количестве членов разложения.

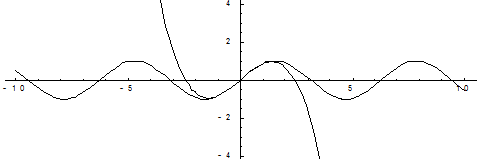
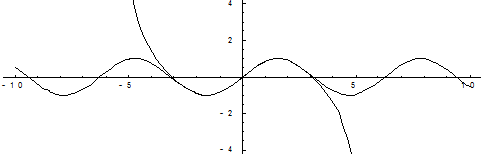
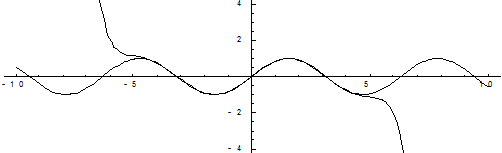
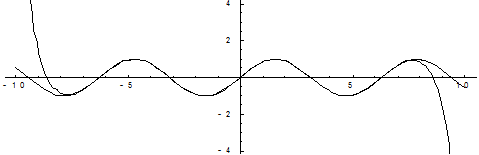
Рис. 4. Десять членов разложения

Чтобы получить наиболее точное значение функции при наименьшем количестве членов разложения надо в формуле Тейлора в качестве параметра а выбрать такое число, которое достаточно близко к значению х, и значение функции от этого числа легко вычисляется.

Для примера вычислим значение sin20⁰.

Предварительно переведем угол 20⁰ в радианы: 20⁰ = p/9.

Применим разложение в ряд Тейлора, ограничившись тремя первыми членами разложения:

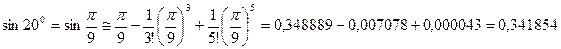
В четырехзначных таблицах Брадиса для синуса этого угла указано значение 0,3420.

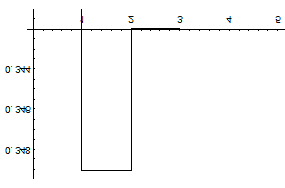
На графике показано изменение значений разложения в ряд Тейлора в зависимости от количества членов разложения. Как видно, если ограничиться тремя членами разложения, то достигается точность до 0,0002.

Выше говорилось, что при х®0 функция sinx является бесконечно малой и может при вычислении быть заменена на эквивалентную ей бесконечно малую функцию х. Теперь видно, что при х, близких к нулю, можно практически без потери в точности ограничиться первым членом разложения, т.е. sinx @ x.

Пример: Вычислить sin28⁰13¢15¢¢.

Для того, чтобы представить заданный угол в радианах, воспользуемся соотношениями:

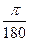1⁰ = ; 28⁰;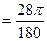

1¢; ;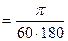

; ;

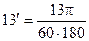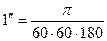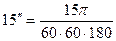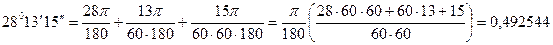рад

Если при разложении по формуле Тейлора ограничиться тремя первыми членами, получим: sinx = .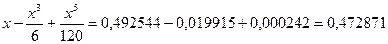

Сравнивая полученный результат с более точным значением синуса этого угла,

sin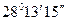= 0,472869017612759812,

видим, что даже при ограничении всего тремя членами разложения, точность составила 0,000002, что более чем достаточно для большинства практических технических задач.

Получаем: f(x) = ln(1 + x); f (0) = 0;

f¢(x) = ;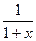

………………………………………

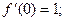
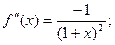
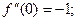
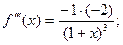
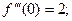
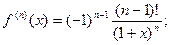
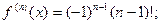
Итого: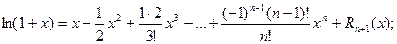

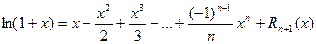
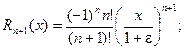
Полученная формула позволяет находить значения любых логарифмов (не только натуральных) с любой степенью точности. Ниже представлен пример вычисления натурального логарифма ln1,5. Сначала получено точное значение, затем – расчет по полученной выше формуле, ограничившись пятью членами разложения. Точность достигает 0,0003.

ln1,5 = 0,405465108108164381

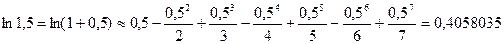
Разложение различных функций по формулам Тейлора и Маклорена приводится в специальных таблицах, однако, формула Тейлора настолько удобна, что для подавляющего большинства функций разложение может быть легко найдено непосредственно.

Ниже будут рассмотрены различные применения формулы Тейлора не только к приближенным представлениям функций, но и к решению дифференциальных уравнений и к вычислению интегралов.

Применение дифференциала к приближенным вычислениям.

Дифференциал функции y = f(x) зависит от Dх и является главной частью приращения Dх.

Также можно воспользоваться формулой

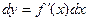
Тогда абсолютная погрешность

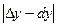
Относительная погрешность

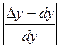
Более подробно применение дифференциала к приближенным вычислениям будет описано ниже.

Теоремы о среднем.

Теорема Ролля.

(Ролль (1652-1719)- французский математик)

Если функция f(x) непрерывна на отрезке [a, b], дифференцируема на интервале (а, b) и значения функции на концах отрезка равны f(a) = f(b), то на интервале (а, b) существует точка e, a < e < b, в которой производная функция f(x) равная нулю,

f¢(e) = 0.

Геометрический смысл теоремы Ролля состоит в том, что при выполнении условий теоремы на интервале (a, b) существует точка e такая, что в соответствующей точке кривой y = f(x) касательная параллельна оси Ох. Таких точек на интервале может быть и несколько, но теорема утверждает существование по крайней мере одной такой точки.

Доказательство. По свойству функций, непрерывных на отрезке функция f(x) на отрезке [a, b] принимает наибольшее и наименьшее значения. Обозначим эти значения М и m соответственно. Возможны два различных случая М = m и M ¹ m.

Пусть M = m. Тогда функция f(x) на отрезке [a, b] сохраняет постоянное значение и в любой точке интервала ее производная равна нулю. В этом случае за e можно принять любую точку интервала.

Пусть М = m. Так значения на концах отрезка равны, то хотя бы одно из значений М или m функция принимает внутри отрезка [a, b]. Обозначим e, a < e < b точку, в которой f(e) = M. Так как М- наибольшее значение функции, то для любого Dх (будем считать, что точка e + Dх находится внутри рассматриваемого интервала) верно неравенство:

Df(e) = f(e + Dx) – f(e) £ 0

При этом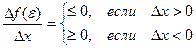

Но так как по условию производная в точке e существует, то существует и предел .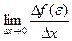

Т.к. 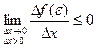и 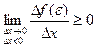, то можно сделать вывод:

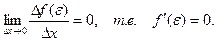
Теорема доказана.

Теорема Ролля имеет несколько следствий:

1) Если функция f(x) на отрезке [a, b] удовлетворяет теореме Ролля, причем

f(a) = f(b) = 0, то существует по крайней мере одна точка e, a < e < b, такая, что f¢(e) = 0. Т.е. между двумя нулями функции найдется хотя бы одна точка, в которой производная функции равна нулю.

2) Если на рассматриваемом интервале (а, b) функция f(x) имеет производную (n-1)- го порядка и n раз обращается в нуль, то существует по крайней мере одна точка интервала, в котором производная (n – 1) – го порядка равна нулю.

Теорема Лагранжа.

(Жозеф Луи Лагранж (1736-1813) французский математик)

Если функция f(x) непрерывна на отрезке [a, b] и дифференцируема на интервале (а, b), то на этом интервале найдется по крайней мере одна точка e

a < e < b, такая, что .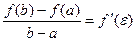

Это означает, что если на некотором промежутке выполняются условия теоремы, то отношение приращения функции к приращению аргумента на этом отрезке равно значению производной в некоторой промежуточной точке.

Рассмотренная выше теорема Ролля является частным случаем теоремы Лагранжа.

Отношение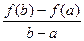равно угловому коэффициенту секущей АВ.

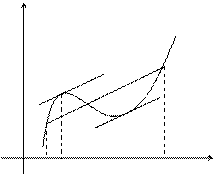у

В

А

0 а e b x

Если функция f(x) удовлетворяет условиям теоремы, то на интервале (а, b) существует точка e такая, что в соответствующей точке кривой y = f(x) касательная параллельна секущей, соединяющей точки А и В. Таких точек может быть и несколько, но одна существует точно.

Доказательство. Рассмотрим некоторую вспомогательную функцию

F(x) = f(x) – y_{сек АВ}

Уравнение секущей АВ можно записать в виде:

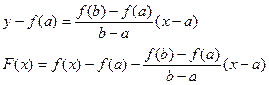
Функция F(x) удовлетворяет теореме Ролля. Действительно, она непрерывна на отрезке [a, b] и дифференцируема на интервале (а, b). По теореме Ролля существует хотя бы одна точка e, a < e < b, такая что F¢(e) = 0.

Т.к. 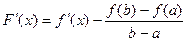, то 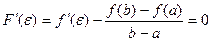, следовательно

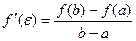
Теорема доказана.

Дата добавления: 2013-12-11