Обработка и анализ результатов моделирования систем

Таблица 6.7

.

Общая совокупность таких векторов 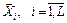образует план эксперимента, а совокупность различных векторов, число которых обозначим N, – спектр плана.

В активном эксперименте факторы могут принимать только фиксированные значения. Фиксированное значение фактора называют уровнем фактора. Количество принимаемых уровней факторов зависит от выбранной структуры факторной модели и принятого плана эксперимента. Минимальный 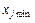и максимальный 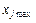, 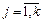(k – число факторов) уровни всех факторов выделяют в факторном пространстве некоторый гиперпараллелепипед, представляющий собой область планирования. В области планирования находятся все возможные значения факторов, используемые в эксперименте.

Вектор 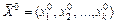задает точку центра области планирования. Координаты этой точки 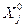обычно выбирают из соотношения

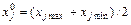. (6.1)

Точку 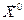называют центром эксперимента. Она определяет основной уровень факторов 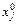, 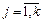. Центр эксперимента стремятся выбрать как можно ближе к точке, которая соответствует искомым оптимальным значениям факторов. Для этого используется априорная информация об объекте.

Интервалом (или шагом) варьирования фактора x_j называют величину, вычисляемую по формуле

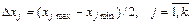(6.2)

Факторы нормируют, а их уровни кодируют. В кодированном виде верхний уровень обозначают +1, нижний – 1, а основной 0. Нормирование факторов осуществляют на основе соотношения

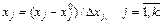(6.3)

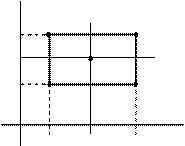
Для переменных 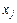,начало координат совмещено с центром эксперимента, а в качестве единиц измерения используются интервалы варьирования факторов. Геометрическое представление области планирования при двух факторах показано на рис. 6.3. Центр эксперимента находится в точке 0 с координатами 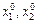. Точки 1, 2, 3, 4 являются точками плана эксперимента. Например, значения факторов x ₁ и x ₂ в точке 1 равны соответственно 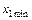и 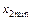, а нормированные их значения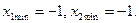

В дальнейшем будем предполагать, что в планах активных экспериментов факторы нормированы.

План эксперимента удобно представлять в матричной форме. План эксперимента задается либо матрицей плана, либо матрицей спектра плана в совокупности с матрицей дублирования.

х ₂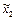

х _2max 3 +1 4

D х ₂

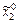– 1 0 +1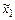

х _2min 1 – 1 2

0 х _1min 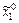х _{1 max} х ₁

Рис. 6.3. Геометрическое представление области планирования при двух факторах: x ₁ и x ₂

Матрица плана представляет собой прямоугольную таблицу, содержащую информацию о количестве и условиях проведения опытов. Строки матрицы плана соответствуют опытам, а столбцы – факторам. Размерность матрицы плана L х k, где L – число опытов, k – число факторов. При проведении повторных (дублирующих) опытов в одних и тех же точках плана матрица плана содержит ряд совпадающих строк.

Матрица спектра плана – это матрица, в которую входят только различающиеся между собой строки матрицы плана. Размерность матрицы спектра плана N х k, где N – число точек плана, различающихся между собой хотя бы одной координатой .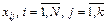

Матрица спектра плана имеет вид

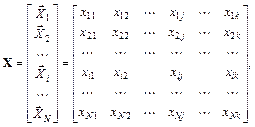(6.4)

где 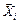– вектор, определяющий нормированные значения координат точки плана в i -м опыте; x_ij – нормированное значение j -го фактора в i -м опыте.

Матрица дублирования – квадратная диагональная матрица n, диагональные элементы которой равны числам параллельных опытов в соответствующих точках спектра плана:

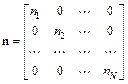. (6.5)

Опыты при выполнении эксперимента проводятся в последовательности, предусмотренной матрицей плана. Эта матрица составляется лишь при необходимости рандомизации опытов, когда в результатах эксперимента можно ожидать наличие систематических ошибок. Для выбора случайной последовательности опытов используется таблица равномерно распределенных случайных чисел. Первое число таблицы выбирают произвольно, желательно случайным образом, а затем, начиная с этого числа, выписывают L чисел таблицы, где L – число опытов (с учетом их дублирования). При этом числа, большие L, а также уже выписанные, отбрасываются.

В вычислительных экспериментах опыты проводят в соответствии с матрицей спектра плана, так как предполагается отсутствие систематических ошибок и поэтому нет необходимости в рандомизации опытов.

Определение базисных функций с помощью регрессионного анализа. Регрессионный анализ проводится с целью получения по экспериментальным данным регрессионных моделей, представляющих собой экспериментальные факторные модели. Задачей регрессионного анализа является определение параметров экспериментальных факторных моделей объектов проектирования или исследования, т.е. определение коэффициентов уравнений моде­лей при выбранной их структуре.

Регрессионный анализ включает три основных этапа:

1) статистический анализ результатов эксперимента;

2) получение оценок 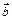искомых коэффициентов регрессии ;

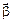3) оценку адекватности и работоспособности полученной экспериментальной факторной модели технической системы.

Под структурой экспериментальной факторной математической модели понимается вид математических соотношений между факторами X, V и откликом Y. В качестве факторов принимают внутренние и внешние параметры технической системы, подлежащие оптимизации в процессе ее проектирования. Внутренние параметры системы – это параметры ее элементов, внешние – это параметры внешней среды, в условиях воздействий которой осуществляется функционирование системы. Функциями отклика Y являются выходные параметры технической системы, характеризующие ее эффективность и качество процессов функционирования. Выходные параметры системы принимаются в качестве критериев оптимальности.

Как уже отмечалось, структура факторной модели выбирается на основе априорной информации, используя принцип постепенного ее усложнения. Параметры факторной математической модели определяются методами регрессионного анализа. При определении параметров этими методами нет необходимости различать виды факторов, т. е. подразделять факторы на управляемые Х и неуправляемые V. Поэтому в дальнейшем все они будут обозначаться буквой Х. Тогда факторную модель можно представить векторным уравнением регрессии вида

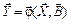. (6.6)

Определение параметров В этой модели будем рассматриватьна примере одного уравнения 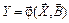. Для определения параметров используются результаты эксперимента. Результаты эксперимента можно представить функцией вида

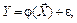(6.7)

где 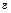– аддитивная помеха случайного характера с нормальным законом распределения.

Так как каждый опыт проводится при определенном сочетании уровнейфакторов X, то функцию 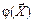представим выражением

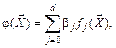(6.8)

где 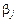– j- й элемент вектора искомых коэффициентов уравнения регрессии: 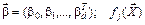– j- я базисная функция – элемент вектора базисных функций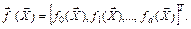

В качестве базисных функций используют полиномы простейших переменных, системы ортогональных полиномов, тригонометрические функции. Наиболее часто пользуются полиномами первой и второй степеней. Например, полином первой степени, описывающий функцию отклика у при двух факторах x ₁ и x ₂, может иметь вид

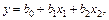(6.9)

или

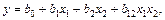(6.10)

а полином второй степени

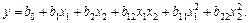
(6.11)

Базисные функции в случае использования последнего выражения имеют вид:.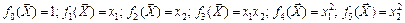

Если уравнение регрессии имеет вид выражений (6.9), (6.10), его называют уравнением линейной регрессии (линейной регрессией или регрессией первого порядка), а если содержит факторы во второй и более высокой степени – нелинейной регрессией (регрессией соответствующего порядка).

Линейная регрессия может представлять как линейную математическую модель, так и нелинейную, в зависимости от того, содержит ли она линейные эффекты (как в выражении(6.9),или наряду с ними также эффекты взаимодействия (как в выражении (6.10)). Линейным называют эффект, характеризующий линейную зависимость выходного параметра у от соответствующего фактора x_i. Эффектом взаимодействия называют эффект, характеризующий совместное влияние нескольких факторов на у (например, в выражении (6.10) 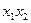). Эффекты взаимодействия двух факторов называют парным взаимодействием, трех факторов – тройным взаимодействием и т.д.

Как всякий статистический метод, регрессионный анализ применим при определенных предпосылках (постулатах).

1. Аддитивная помеха 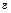– случайная нормально распределенная величина с параметрам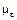и =0 и 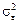=const. В этом случае функция отклика Y также случайная величина с нормальным законом распределения. Гипотезу о нормальном распределении Y можно проверить по критерию Пирсона.

2. Постоянство дисперсии помехи означает, что интенсивность ошибки определения Y не меняется при изменении уровня факторов в процессе эксперимента. Выполнение этого постулата проверяется по критерию однородности дисперсии в разных точках опыта.

3. Значения факторов в активном эксперименте – неслучайные величины. Это означает, что установление каждого фактора на заданном уровне и удерживание его на этом уровне во время опыта точнее, чем ошибка воспроизводимости. В вычислительном эксперименте это выполняется однозначно, а в физическом вклад, вносимый ошибками измерения факторов Х, должен быть пренебрежимо малым в сравнении с действием других неконтролируемых факторов, образующих ошибку e определения функции Y.

4. Значения помехи e в различных точках опыта некоррелированы. Для обеспечения этих требований используется рандомизация опытов. В пассивном эксперименте условие некоррелированости помехи обеспечивают путем соответствующего выбора временного интервала съема информации об условиях и результатах опытов.

5. Векторы-столбцы базисных функций должны быть линейно независимыми. Выполнение этого требования необходимо для получения раздельных оценок 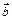всех коэффициентов регрессии 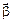. В активном эксперименте оно обеспечивается соответствующим выбором спектра плана эксперимента. При этом число опытов N (без учета дублирования) должно быть не меньше, чем число оцениваемых коэффициентов N_B, т. е. N≥N_B.

В пассивном эксперименте линейная зависимость между столбцами практический исключается, так как факторы неуправляемы и принимают случайные значения в различных опытах, но может наблюдаться сильная коррелированность столбцов, что повлечет за собой большие ошибки вычисления коэффициентов регрессии. Для выявления коррелированности столбцов проводят корреляционный анализ результатов пассивного эксперимента.

Оценка параметров регрессионной модели. Исходными данными для получения оценок параметров регрессионной модели технической системы (т.е. оценок 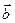искомых коэффициентов регрессии 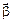) является информация о значениях управляемых факторов 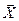(или неуправляемых – при проведении пассивного эксперимента) и функции отклика Y. Эту информацию можно представить в виде матрицы X значений факторов во всех N опытах, предусмотренных спектром плана эксперимента, и вектора-столбца 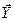полученных в этих опытах значений функции отклика Y:

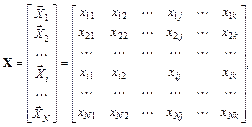(6.12)

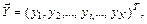(6.13)

где 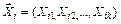– вектор-строка значений факторов в i -м опыте; x_ij – значение j- го фактора в i -м опыте; k – количество факторов; N – количество опытов; 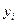– значение функции отклика Y в i -м опыте (если проводились параллельные опыты, т. е. осуществлялось дублирование опытов, то вместо 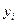используются оценки их математических ожиданий, т.е. выборочные средние ).

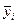Значения базисных функций во всех опытах представляют собой матрицу F, называемую матрицей базисных функций

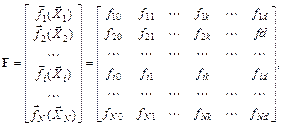(6.14)

где 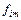– значение m -ой базисной функции в i -м опыте; 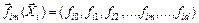– вектор-строка значений базисных функций в i- м опыте.

Используя информацию об X, 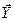и F, необходимо найти оценки коэффициентов регрессии, представляемые вектором-столбцом

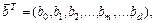(6.15)

где b_k – значение оценки коэффициента регрессии при базисной функции .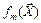

Так как функция отклика Y – случайная величина, поскольку на ее значения в различных опытах оказывает влияние случайная помеха ε, то оценки коэффициентов регрессии будут случайными величинами.

Уравнение регрессии устанавливает зависимость между оценкой математического ожидания функции отклика 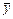и факторами 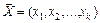. Общий вид этой зависимости

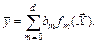(6.16)

В связи с наличием помехи значение функции отклика в i- м опыте 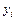будет отличаться от 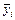. Для определения 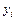можно составить выражение

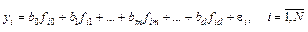, (6.17)

где ε _i - невязка уравнения регрессии в i- м опыте.

Невязка характеризует отклонение значений функции отклика в опытах от получаемых с помощью регрессионной модели (6.16). Она возникает по двум причинам: из-за ошибки эксперимента и из-за непригодности (приближенности) выбранной структуры факторной математической модели. Причем эти причины смешаны и нельзя сказать, какая из них преобладает.

Если постулировать, что модель пригодна, то невязка будет порождаться только ошибкой опыта. Тогда для определения коэффициентов уравнения (6.16) невязку надо минимизировать. Для этого в регрессионном анализе используется метод наименьших квадратов (МНК). Составляется функция, представляющая собой сумму квадратов невязок, и осуществляется ее минимизация, т.е.

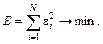(6.18)

Подставим значение ε _i из выражения (6.17)

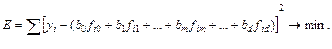(6.19)

В выражении (6.19) коэффициенты b_m рассматриваются как неизвестные переменные, которые наилучшим образом соответствуют полученным результатам эксперимента. Значения этих коэффициентов, при которых достигается минимум функции Е, принимаются в качестве оценок коэффициентов регрессии. Минимум функции Е имеет место при равенстве нулю частных производных этой функции по переменным b ₀, b ₁, …, b_d:

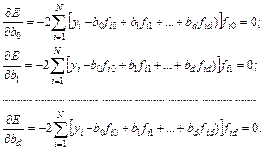
После преобразований получим систему линейных неоднородных алгебраических уравнений относительно искомых оценок коэффициентов регрессии b ₀, b ₁, …, b_d:

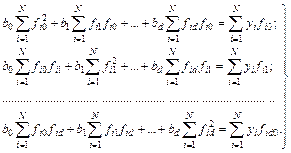(6.20)

Очевидно, что коэффициенты при неизвестных переменных 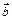этой системы уравнений являются элементами матрицы Ф, определяемой из выражения

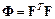, (6.21)

в котором F представляет собой матрицу базисных функций (6.14). Значения элементов матрицы F известны из проведенного эксперимента. Следовательно, элементы матрицы Ф оказываются известными коэффициентами системы уравнений (6.20). Выпишем матрицу Ф

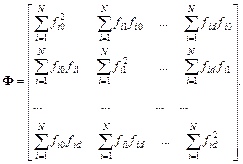(6.22)

Матрицу Ф называют информационной матрицей Фишера. Она содержит (d +1) строк и (d +1) столбцов, причем, элемент j -й строки m -го столбца представляет собой сумму 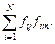Матрица Ф симметрична относительно главной диагонали, что упрощает составление системы алгебраических уравнений (6.20) для регрессионной модели.

Систему уравнений (6.20) можно также записать в матричной форме

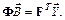(6.23)

Система уравнений (6.20) имеет единственное решение, если определитель матрицы Ф не равен нулю. В этом случае матрица Ф будет невырожденной. Выполнение пятой предпосылки регрессионного анализа, изложенной в предыдущем параграфе, исключает возникновение вырожденности.

Решение системы уравнений (6.20) обычно осуществляют методом Гаусса. При небольшом числе определяемых коэффициентов b_k можно использовать правило Крамера.

Полученные методом наименьших квадратов оценки b ₀, b ₁, …, b_d действительных значений коэффициентов регрессии β₀, β₁…, β _d обладают следующими свойствами:

1) математические ожидания оценок 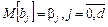, т. е. оценки b_j несмещенные;

2) дисперсии оценок коэффициентов регрессии минимальны и равны

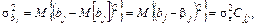(6.24)

а корреляционный момент

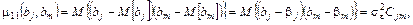(6.25)

где C_jj, C_jm – элементы матрицы Ф ^-1, обратной к информационной; 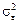– дисперсия случайной помехи;

3) оценки b ₀, b ₁, …, b_d подчиняются совместному (d + 1)-мерному нормальному распределению.

Планы экспериментов и их свойства. Для проведения активных экспериментов разработано множество различных планов. Планы учитывают как особенности структуры регрессионных моделей, так и требования их эффективности с позиций повышения точности получаемых моделей и снижения затрат на проведение эксперимента.

При построении линейных моделей или нелинейных, содержащих только взаимодействия факторов, но без квадратов этих факторов (регрессий первого порядка), каждый фактор можно варьировать только на двух уровнях. Для получения таких моделей используют планы первого порядка.

Известно несколько разновидностей планов первого порядка. Эти планы различаются в зависимости от структуры регрессионной модели. Они предназначены для планирования следующих видов экспериментов:

· однофакторного (классического) эксперимента;

· полного факторного эксперимента;

· дробного факторного эксперимента.

Если в регрессионную модель входят факторы в квадрате или с более высокими степенями, то необходимо не менее трех уровней варьирования факторов. При построении квадратичных моделей применяют планы второго порядка. Эти планы часто используют в качестве своего ядра какой-либо план первого порядка, который дополняется так называемыми звездными точками.

Планы различают по степени насыщенности. План называют насыщенным, если общее число точек плана равно числу неизвестных параметров регрессионной модели. Такой план позволяет получить экспериментальную факторную модель при минимальных затратах, так как обеспечивает минимум числа опытов.

План называется композиционным, если в спектр его в качестве составной части входят точки спектра плана, который был реализован при построении более простой модели. Композиционность плана позволяет реализовать принцип постепенного усложнения модели при минимальных затратах, так как при этом используются результаты опытов, выполненных для получения простой модели. Многие планы второго порядка являются композиционными.

Важным свойством плана является его ортогональность. У ортогональных планов информационная матрица Фишера Ф диагональная, а столбцы матрицы базисных функций F попарно ортогональны. Для ортогонального плана при заданных значениях диагональных элементов матрицы Ф дисперсии 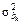оценок коэффициентов регрессии b_k минимальны. Причем эти оценки получаются независимыми, что существенно облегчает их вычисление и анализ.

При изменении вида плана изменяется матрица Ф, что влияет на дисперсии оценок коэффициентов регрессии. Различают D -, А - и E -оптимальные планы. Они обеспечивают различные формы эллипсоидов рассеивания оценок. D -оптимальный план минимизирует обобщенную дисперсию оценок коэффициентов регрессии и обеспечивает минимальный объем эллипсоида их рассеивания. А -оптимальный план минимизирует среднюю дисперсию всех оценок, а эллипсоид имеет наименьшую сумму квадратов длин осей. Эллипсоид рассеивания у Е -оптимального плана имеет минимальную длину своей наибольшей оси.

В зависимости от возможностей предсказания отклика по уравнению регрессии различают планы ротатабельные и униформные. План называется ротатабельным, если дисперсия предсказания отклика постоянна на фиксированном расстоянии от центра эксперимента. Униформный план обеспечивает практически постоянное ее значение в некоторой области факторного пространства. Свойства ротатабельности или униформности обеспечиваются соответствующим выбором точек матрицы спектра плана. Задача выбора оптимального плана довольно сложная и в большинстве случаев не имеет аналитического решения. Поэтому поиск оптимальных планов обычно осуществляется численными методами на ЭВМ.

Рассмотрим основы построения и основные свойства планов первого порядка.

План однофакторного эксперимента. Однофакторный (классический) эксперимент предназначен для получения линейной экспериментальной факторной модели вида

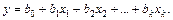(6.26)

Однофакторный эксперимент предусматривает поочередное варьирование каждого из факторов при фиксированных на некотором уровне значениях остальных факторов. Фактор x_i варьируют на двух уровнях x_{i в} и x_{i н}, а все остальные при этом должны находиться в точке центра эксперимента 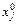, 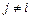. Для нормированных факторов х_{i в} = +1, х_{i н} = – 1, х_j = 0. С учетом этого составим матрицу спектра плана однофакторного эксперимента

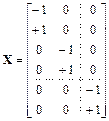(6.27)

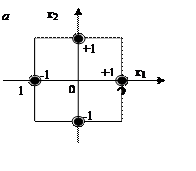
Число точек плана в этом случае N = 2k, где k – количество факторов. Точки спектра плана располагаются в центрах граней гиперкуба.
На рис. 6.4, а показано расположение точек для двумерного случая, а
на рис. 6.4, б — для трехмерного.

Вектор базисных функций имеет вид

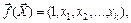(6.28)

а матрица F численных значений базисных функций отличается от матрицы спектра плана Х только одним дополнительным столбцом, соответствующим базисной функции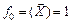

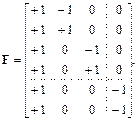(6.29)

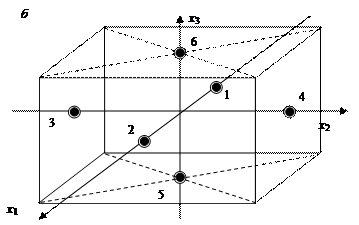Рис. 6.4. Расположение точек спектра однофакторного эксперимента:

а – при двух факторах; б – при трех факторах

Матрица базисных функций F обладает очевидными свойствами:

1) 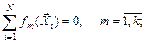(6.30)

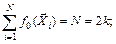(6.31)

2) 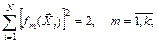(6.32)

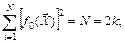(6.33)

3) 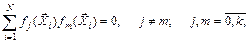(6.34)

где N – число точек спектра плана; 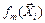– значение m -й базисной функции в i -м опыте.

Согласно выражению (6.34) векторы-столбцы всех базисных функций попарно ортогональны.

Используя свойства (6.32) – (6.34) и выражение (6.22), легко составить информационную матрицу Фишера Ф = F ^T F

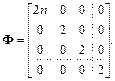(6.35)

Так как матрица Ф диагональная, то план однофакторного эксперимента ортогональный и коэффициенты регрессии некоррелированы друг с другом. Для определения дисперсии оценок коэффициентов регрессии (6.26) вычислим обращенную матрицу Фишера.

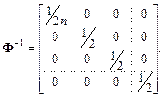(6.36)

Искомые дисперсии оценок коэффициентов регрессии определяются произведениями дисперсии помехи 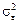на соответствующие диагональные элементы матрицы Ф ^-1:

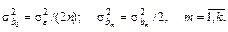(6.37)

Очевидно, что точность получаемой модели в этом случае невысокая, так как коэффициенты регрессии b_m, 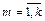(кроме коэффициента b ₀) имеют высокое значение дисперсии. Поэтому однофакторный эксперимент следует признать явно неудовлетворительным для построения модели технической системы. В связи с этим в настоящее время он практически не применяется. Следует отметить, что рассмотренный план обладает свойством ротатабельности.

План полного факторного эксперимента. Спектр плана полного факторного эксперимента (ПФЭ) содержит все возможные комбинации значений факторов на всех уровнях их изменения. Число точек N спектра плана определяется по формуле

N=q^k, (6.38)

где q – число уровней варьирования факторов; k – количество факторов.

Рассмотрим особенности и свойства ПФЭ, применяемых при построении линейных регрессий вида

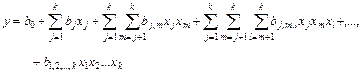(6.39)

Для получения линейной регрессии достаточно варьировать факторы на двух уровнях, т. е. q = 2. Тогда число точек спектра плана будет

N= 2 ^k. (6.40)

Такой план принято обозначать ПФЭ2 ^k.

Рассмотрим порядок составления матрицы спектра плана, полагая, что факторы нормированы и, следовательно, могут принимать значения только либо +1, либо – 1. Напомним, что столбцы матрицы Х соответствуют значениям факторов x ₁, x ₂, …, x_k.

Для составления матрицы спектра плана используется следующее простое правило: в первой строке матрицы все факторы равны – 1, в первом столбце знаки единиц меняются поочередно; во втором столбце они чередуются – через 2; в третьем – через 4; в четвертом – через 8 и т. д. по степеням двойки. Следовательно, для каждого последующего столбца частота изменения знака в два раза меньше, чем для предыдущего.

Используя изложенное правило чередования знаков, составим матрицы спектров планов для случаев k = 2 и k = 3, т. е. для двух и трех факторов.

При k = 2 число точек плана N = 2² = 4, а матрица спектра плана имеет вид

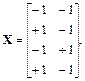(6.41)

при n= 3 N= 2³=8, а матрица X

(6.42)

Спектры планов можно изобразить в привычной для экспериментатора табличной форме. В табл. 6.1 приведен спектр плана ПФЭ2², а в табл. 2 – спектр плана ПФЭ2³.

Таблица 6.1

i	Факторы
x 1	x 2
	-1	-1
	+1	-1
	-1	+1
	+1	+1

Таблица 6.2

i	Факторы
X 1	x 2	x 3
	-1	-1	-1
	+1	-1	-1
	-1	+1	-1
	+1	+1	-1
	-1	-1	+1
	+1	-1	+1
	-1	+1	+1
	+1	+1	+1

В табл. 1, 2 и в последующем буквой i обозначен номер точки спектра плана.

Точки плана ПФЭ2 ^k располагаются в вершинах k -мерного гиперкуба. На рис. 6.4, а показано расположение точек для двумерного случая, а
на рис.6.5, б – для трехмерного.

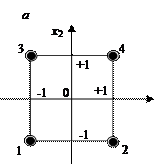
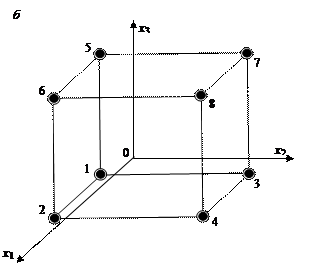
Рис.6.5. Расположение точек спектра плана ПФЭ2 ^k:

а – при k = 2; б – при k = 3

Посредством ПФЭ можно построить как простейшую линейную модель технической системы вида

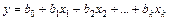, (6.43)

так и нелинейную.

Для модели вида (6.43) система базисных функций очевидна:

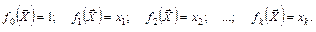
Число базисных функций в этом случае равно k + 1.

Выясним, какие базисные функции могут входить в регрессионную модель, получаемую посредством ПФЭ2 ^k, чтобы выполнялось требование о линейной независимости векторов-столбцов этих функций. При выполнении этого требования получают раздельные оценки всех коэффициентов регрессии. Линейная независимость столбцов матрицы F достигается, если в ней отсутствуют полностью совпадающие или полностью противоположные (по знакам) столбцы.

В общем случае в полиномиальную модель могут входить факторы в любой степени и различные комбинации из их произведений. Так как при нормированных факторах их значения равны – 1 или +1, а в качестве показателей степеней факторов принимаются целые числа, то при четных показателях степеней вектор-столбец базисной функции состоит только из +1 и совпадает с вектором-столбцом функции 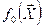, а векторы-столбцы всех базисных функций, соответствующих одним и тем же факторам х_j, возведенным в любые нечетные степени, будут совпадающими. Вместе с тем легко убедиться, что любые комбинации произведений факторов x ₁, x ₂, …, x_k могут быть в числе базисных функций.

Выпишем выражения линейных регрессий при k = 2 с учетом всех возможных сочетаний взаимодействия факторов

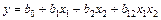. (6.44)

При k = 3 получаем

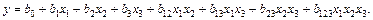(6.45)

В табл. 6.3 приведены базисные функции плана ПФЭ2², используемого для построения регрессионной модели (6.44), а в табл. 6.4 – плана ПФЭ2³, используемого для модели (6.45). Прямоугольниками в этих таблицах обведены спектры планов.

Таблица 6.3

i	f 0=1	f 1= x 1	f 2= x 2	f 3= x 1 x 2
	+1	-1	-1	+1
	+1	+1	-1	-1
	+1	-1	+1	-1
	+1	+1	+1	+1

Таблица 6.4

i	f 0=1	f 1= x 1	f 2= x 2	f 3= x 3	f 4= x 1 x 2	f 5= x 1 x 3	f 6= x 2 x 3	f 7= x 1 x 2 x 3
	+1	-1	-1	-1	+1	+1	+1	-1
	+1	+1	-1	-1	-1	-1	+1	+1
	+1	-1	+1	-1	-1	+1	-1	+1
	+1	+1	+1	-1	+1	-1	-1	-1
	+1	-1	-1	+1	+1	+1	-1	+1
	+1	+1	-1	+1	-1	-1	-1	-1
	+1	-1	+1	+1	-1	+1	+1	-1
	+1	+1	+1	+1	+1	-1	+1	+1

Уравнение линейной регрессии, как это видно из (6.39) и (6.45), может содержать следующее предельное количество коэффициентов при различных видах базисных функций:

· один коэффициент b ₀ – свободный член уравнения регрессии;

· п коэффициентов b_j – линейных членов уравнения регрессии;

· С_n ²коэффициентов b_j,m при парных взаимодействиях факторов;

· С_n ³ коэффициентов b_j,m,l при тройных взаимодействиях факторов и т. д.;

· один коэффициент b _{1,2,…, k} при взаимодействии факторов максимального, k -го порядка.

Выражение для определения общего числа коэффициентов регрессии имеет вид

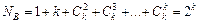. (6.46)

Так как при использовании всех возможных сочетаний факторов в уравнении регрессии число определяемых коэффициентов N_B равно числу точек N спектра плана ПФЭ2 ^k, то такой план является насыщенным.

Численные значения 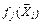, приведенные в таблице базисных функций, являются элементами матрицы F. Матрица F плана ПФЭ2 ^k обладает следующими свойствами.

1. Свойство симметричности относительно центра эксперимента – алгебраическая сумма элементов каждого столбца матрицы базисных функций, кроме столбца 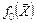, равна нулю

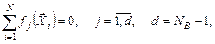(6.47)

где 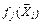– значение j -й базисной функции, соответствующее i -й строке матрицы F; i – номер точки спектра плана; N – число точек спектра плана;
N_B – количество базисных функций.

2. Свойство ортогональности столбцов – сумма построчных произведений элементов любых двух столбцов равна нулю

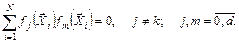(6.48)

3. Свойство нормировки – сумма квадратов элементов каждого столбца матрицы базисных функций равна числу точек N спектра плана

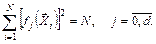(6.49)

4. Для столбца базисной функции 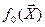сумма элементов также равна N

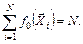(6.50)

Выражения (6.47) – (6.50) записаны в предположении, что дублирование опытов не производится.

Составим информационную матрицу Фишера Ф, определяемую выражением (6.22). Выражения (6.48) и (6.49) позволяют определить элементы матрицы Ф. Очевидно, что для IIФЭ2 ^k матрица Ф диагональная с постоянными диагональными элементами

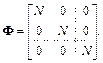(6.51)

Следовательно, ПФЭ2 ^k относятся к классу ортогональных планов.

Так как матрица Ф диагональная, то корреляционные моменты оценок коэффициентов регрессии 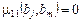и оценки всех коэффициентов регрессии b_j, j =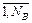некоррелированы друг с другом. Кроме того, все коэффициенты регрессии оцениваются с одинаковой точностью, так как диагональные элементы матрицы Ф одинаковы. Дисперсия оценок коэффициентов

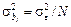. (6.52)

Для линейной модели вида (6.43) план ПФЭ2 ^k является А - и E -оптимальным и ротатабельным, а для модели (6.39) – D- оптимальным.

План дробного факторного эксперимента. Наряду с отмеченными положительными качествами полного факторного эксперимента он имеет существенный недостаток: увеличение количества факторов приводит к быстрому росту числа опытов, что обусловлено степенной зависимостью (6.38). Например, при k = 10 спектр плана содержит N = 2¹⁰ = 1024 опыта. Кроме того, необходимо дублирование опытов.

ПФЭ позволяет построить регрессионную модель, которая учитывает влияние на функцию отклика выбранных факторов и всех возможных сочетаний взаимодействий этих факторов. Но поскольку структура модели выбирается на основе априорной информации о физических свойствах исследуемого объекта, то весьма сложно представить себе влияние на характеристики его функционирования эффектов взаимодействий выше второго или третьего порядка. Обычно при построении многофакторной регрессионной модели ограничиваются парными или, в крайнем случае, отдельными тройными взаимодействиями факторов. В этом случае ПФЭ оказывается избыточным, так как число точек спектра плана N значительно больше количества коэффициентов регрессии N_B. В результате возникает возможность сокращения числа опытов. Но при этом, естественно, должно соблюдаться условие возможности оценки коэффициентов регрессии по результатам опытов, которое выражается соотношением N ≥ N_B.

Во многих случаях на начальной стадии моделирования технической системы в связи с отсутствием необходимой информации о влиянии на ее выходные параметры различных факторов (внутренних или внешних параметров) строят линейную модель вида (6.43). Например, при трех факторах выбирают модель в виде

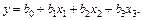(6.53)

В этом уравнении четыре коэффициента регрессии, а при k = 3 спектр плана ПФЭ, согласно выражению (6.40), содержит 8 точек, т.е. предусматривает 8 опытов в различных точках факторного пространства. Следовательно, четыре опыта оказываются избыточными и их можно было бы исключить, естественно, при условии выполнения принятых предпосылок регрессионного анализа, прежде всего ортогональности столбцов матрицы базисных функций F.

При построении математических моделей, использующих упрощенные уравнения регрессий, когда N > N_B, применяют дробные факторные эксперименты (ДФЭ). Наибольшее распространение имеют регулярные планы ДФЭ типа 2 ^k-p, т. е. ДФЭ2 ^k-p, где k – число факторов, р – степень дробности ДФЭ. Планы ДФЭ принято называть репликами с указанием их степени дробности. Так, план ДФЭ2 ^{k -1} называют полурепликой ПФЭ2 ^k (1/2-реплика); ДФЭ2 ^{k -2} – 1/4-реплика ПФЭ2 ^k; ДФЭ2 ^{k -3} – 1/8-реплика ПФЭ2 ^k и т.д. Полуреплика сокращает число опытов в два раза по сравнению с ПФЭ, 1/4-реплика – в четыре раза и т.д.

При построении матрицы спектра плана ДФЭ2 ^k-p необходимо обеспечить выполнение условий, описываемых выражениями (6.47) – (6.50), принимая во внимание, что число точек спектра этого плана определяется по формуле

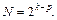(6.54)

Условия (6.47) – (6.50) удовлетворяются, если в матрице базисных функций F отсутствуют полностью совпадающие или полностью противоположные столбцы, что позволяет получить раздельное оценивание всех коэффициентов регрессии.

При выборе степени дробности ДФЭ должно выполняться условие

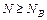. (6.55)

Выбранные базисные функции для ДФЭ составляют лишь некоторую часть базисных функций соответствующего ПФЭ. Назовем эти функции существенными переменными, характеризующими в наибольшей мере физические свойства технического объекта.

Процедура построения спектра плана ДФЭ2 ^k-p содержит четыре этапа.

Этап 1. Выбор структуры уравнения регрессии и определение степени дробности ДФЭ. При этом исходят из условия выполнения
соотношения (6.55).

Этап 2. Выбор ведущих факторов и построение для них матрицы спектра плана, определяющего программу их изменения в ходе эксперимента.

Число m ведущих факторов принимают равным разности между количеством факторов п и степенью дробности ДФЭ

m=k – p. (6.56)

Для выбранных ведущих факторов x ₁, x ₂ ,…, x_m строят план ПФЭ2 ^m, используя изложенное в предыдущем параграфе правило чередования знаков.

Этап 3. Построение матрицы Х спектра плана ДФЭ2 ^k-p. Часть этой матрицы составляет матрица спектра плана ПФЭ2 ^m, а во вторую часть должны войти столбцы матрицы для остальных факторов x_{m+ 1}, x_{m +2} ,…, x_k, количество которых равно

р = k – m. (6.57)

Столбцы матрицы X, соответствующие этим факторам, определяют путем перемножения соответствующих столбцов ведущих факторов. Для этого используют генерирующие соотношения. Генерирующим соотношением называется алгебраическое выражение, устанавливающее связь между одним из факторов x_{m+ 1}, x_{m +2},…, x_k и произведением какой-либо комбинации ведущих факторов x ₁, x ₂, …, x_m. Пример x_{m +1}= x ₁ x ₂ x ₃.

Чтобы получаемые столбцы были ортогональными, для каждого из них задается отдельное генерирующее соотношение (количество этих соотношений равно р). Выбор генерирующих соотношений, вообще говоря, произволен. Однако в качестве генерирующих нельзя использовать те произведения ведущих факторов, которые входят в состав существенных переменных, так как в этом случае в матрице базисных функций F окажутся совпадающие столбцы: для одного из факторов x_{m+ 1}, x_{m +1}, …, x_k и одного из взаимодействий факторов из числа существенных переменных.

Генерирующее соотношение имеет вид

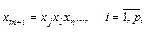(6.58)

где x_m+i – фактор, не включенный в число ведущих (для него определяется столбец матрицы Х спектра плана ДФЭ2 ^k-p); x_j, x_l, x_n, … – ведущие факторы.

Количество ведущих факторов, входящих в генерирующее соотношение (6.58), может быть произвольным, но соотношения (6.58) для всех x_m+i должны быть разными.

Этап 4. Проверка пригодности полученного спектра плана. Для этого необходимо построить матрицу базисных функций F и проверить, нет ли в ней совпадающих или полностью противоположных столбцов, т.е. выяснить, обладает ли матрица F свойством ортогональности столбцов, определяемым выражением (6.48). Если в матрице F нет совпадающих или противоположных столбцов, полученный спектр плана ДФЭ2 ^k-p пригоден для решения поставленной задачи. В противном случае выполняются последовательно следующие процедуры до тех пор, пока не будет обеспечена ортогональность:

· выбираются иные генерирующие соотношения;

· изменяется набор ведущих факторов;

· уменьшается степень дробности плана р.

При ограниченных возможностях проведения опытов степень дробности плана сохраняют, а изменяют структуру уравнения регрессии (например, используют иные взаимодействия факторов или исключают какую-либо базисную функцию, соответствующую одному из взаимодействий высшего порядка).

Таким образом, регулярные планы ДФЭ2 ^k-p обладают теми же свойствами, что и планы ПФЭ2 ^k. Матрица F удовлетворяет выражениям (6.47) – (6.50). Информационная матрица Фишера Ф диагональная и имеет вид (6.51). Дисперсию оценок коэффициентов регрессии определяют по формуле (6.52). Планы ДФЭ2 ^k-p ортогональны. Для линейных моделей они ротатабельны. А - и E- оптимальны, а насыщенные планы D- оптимальны. Поскольку планы ДФЭ значительно экономичнее планов ПФЭ, они получили широкое практическое применение. В частности, их используют для анализа чувствительности целевой функции к вариации параметров технических объектов в процессе их отсеивания и отбора для осуществления оптимизации.

Рассмотрим примеры построения планов ДФЭ.

Пример 1. Получить спектр плана ДФЭ, предназначенного для оценки коэффициентов уравнения регрессии вида (6.53).

Так как число факторов в этом уравнении три (x ₁, x ₂, x ₃), то при проведении ПФЭ количество точек спектра плана было бы равно N =2³=8. В уравнении же (6.53) всего четыре коэффициента, поэтому можно использовать полуреплику, т.е. ДФЭ2^{3 – 1}, спектр плана которой содержит четыре точки: N = 2^{3 – 1} = 4, и следовательно, условие (6.55) выполняется.

Число ведущих факторов m = k – р = 3 – 1 = 2. Выберем в качестве ведущих факторов х ₁ и х ₂ Значения элементов векторов-столбцов этих факторов получим на основе плана ПФЭ2², используя метод чередования знаков. Для определения вектора-столбца фактора x ₃ примем генерирующее соотношение в виде х ₃ = х ₁ х ₂. Полученный спектр плана ДФЭ2^3–1 выделен прямоугольником в табл. 6.5, в которой приведена матрица базисных функций F.

Таблица 6.5

i	f 0=1	f 1= x 1	f 2= x 2	f 3= x 3
	+1 +1 +1 +1	-1 +1 -1 +1	-1 -1 +1 +1	+1 -1 -1 +1

В матрице F нет совпадающих столбцов, следовательно, полученный спектр плана пригоден для решения поставленной задачи.

Пример 2. Задан список существенных переменных: x _1, x ₂, x ₃, x ₄, x ₁ x ₂, x ₂ x ₃, x ₃ x _4. Получить спектр плана ДФЭ.

Уравнение регрессии в этом случае будет включать 4 фактора и 8 коэффициентов, а число точек спектра плана ПФЭ равно N = 2⁴ = 16.

Следовательно, можно попытаться использовать ДФЭ2^4-1, спектр плана которого содержит необходимое число точек N = 8 и обеспечивает выполнение условия (6.55).

Число ведущих факторов m = k – р = 3. Выберем в качестве ведущих факторы x _1, x ₂, x ₃. Для фактора x ₄ необходимо указать генерирующее соотношение. Возможно несколько вариантов: x ₁ x ₂, x ₁ x ₃, x ₂ x ₃, x ₁ x ₂ x ₃. Соотношения x ₁ x ₂ и x ₂ x ₃ принимать нельзя, так как эти взаимодействия факторов входят в список существенных переменных, в результате их вектор-столбцы будут совпадать с вектором-столбцом фактора x ₄. Выберем для начала генерирующее соотношение х ₄ = х ₁ х ₂ х ₃. Вычислив значения элементов столбцов базисных функций f ₄= x _4, f ₅= x ₁ x ₂, f ₆= x ₂ x ₃, f ₇= x ₃ x ₄, получим матрицу F, которая приведена в табл. 6.6. Спектр плана ДФЭ2^4-1 обведен прямоугольником.

Таблица 6.6

i	f 0=1	f 1= x 1	f 2= x 2	f 3= x 3	f 4= x 4= x 1 x 2 x 3	f 5= x 1 x 2	f 6= x 2 x 3	f 7= x 3 x 4
	+1	-1	-1	-1	-1	+1	+1	+1
	+1	+1	-1	-1	+1	-1	+1	-1
	+1	-1	+1	-1	+1	-1	-1	-1
	+1	+1	+1	-1	-1	+1	-1	+1
	+1	-1	-1	+1	+1	+1	-1	+1
	+1	+1	-1	+1	-1	-1	-1	-1
	+1	-1	+1	+1	-1	-1	+1	-1
	+1	+1	+1	+1	+1	+1	+1	+1

Векторы-столбцы 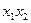и 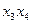оказались одинаковыми, следовательно, полученный план непригоден. Последовательно перебирая все возможные варианты решения проблемы, можно убедиться, что ни один из них не дает положительного результата. Это означает, что при заданном списке существенных переменных план ДФЭ2^4-1 не может быть применен для получения искомого уравнения регрессии. Следовательно, необходимо использовать план ПФЭ2⁴.

Пример 3. Введем небольшое изменение в список существенных переменных примера 2: вместо 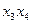примем .

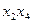Те же действия, что и в предыдущем примере, дают значения элементов матрицы F, приведенные в табл. 6.7.

i	f 0=1	f 1= x 1	f 2= x 2	f 3= x 3	f 4= x 4= x 1 x 2 x 3	f 5= x 1 x 2	f 6= x 2 x 3	f 7= x 3 x 4
	+1	-1	-1	-1	-1	+1	+1	+1
	+1	+1	-1	-1	+1	-1	+1	-1
	+1	-1	+1	-1	+1	-1	-1	+1
	+1	+1	+1	-1	-1	+1	-1	-1
	+1	-1	-1	+1	+1	+1	-1	-1
	+1	+1	-1	+1	-1	-1	-1	+1
	+1	-1	+1	+1	-1	-1	+1	-1
	+1	+1	+1	+1	+1	+

Дата добавления: 2013-12-11