Стоячие волны

Волновое уравнение

Уравнение любой волны является решением дифференциального уравнения, называемого волновым. Чтобы установить вид волнового уравнения, сопоставим вторые частные производные по координатам и времени от функции (11.10), описывающей плоскую волну. Продифференцируем эту функцию дважды по каждой из переменных, получим

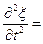-w²a cos(wt-kх+a)=-w²x,

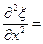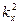-a cos(wt-kх+a)=-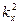x,

Сравнивая эти два выражения и заменив к²/w² через 1/v². Получим уравнение

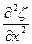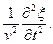= (11.11)

Это и есть волновое уравнение для волны распространяющейся вдоль оси х. В общем случае волновое уравнение имеет вид

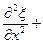
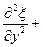
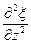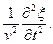= (11.12)

Всякая функция, удовлетворяющая уравнению вида (11.12), описывает некоторую волну, причем корень квадратный из величины, обратной коэффициенту при ¶²x/¶t², дает фазовую скорость этой волны.

Если в среде распространяются одновременно несколько волн, то колебания частиц среды оказываются геометрической суммой колебаний, которые совершали бы частицы при распространении каждой из волн в отдельности. Следовательно, волны просто накладываются одна на другую, не возмущая друг друга. Это утверждение называется принципом суперпозиции (наложения) волн.

В случае, когда колебания, обусловленные отдельными волнами в каждой из точек среды, обладают постоянной разностью фаз, волны называют когерентными. При сложении когерентных волн возникает явление интерференции, заключающееся в том, что колебания в одних точках усиливают, а в других точках ослабляют друг друга.

Очень важный случай интерференции наблюдается при наложении двух встречных волн с одинаковой амплитудой.

Напишем уравнения двух плоских волн, распространяющихся вдоль оси х в противоположных направлениях:

x₁=а cos(wt-kx+a₁), x₂=а cos(wt+kx+a₂).

Сложив вместе эти уравнения и преобразовав результат по формуле суммы косинусов, получим

x=x₁+x₂=2а cos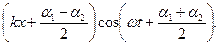 (11.13)

Чтобы упростить его, выберем начало отсчета так, чтобы разность a₂-a₁ стала равной нулю, а начало отсчета t – так, чтобы оказалась равной нулю сумма a₂+a₁. Кроме того, заменим волновое число к его значением 2p/l. Тогда уравнение (11.13) примет вид

x=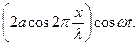 (11.14)

Из (11.14) видно, что в каждой точке стоячей волны происходят колебания той же частоты, что и у встречных волн, причем амплитуда зависит от х:

амплитуда=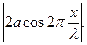

В точках, координаты которых удовлетворяют условию

2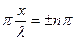 (n=0, 1, 2, …), (11.15)

амплитуда колебаний достигает максимального значения. Эти точки называются пучностями стоячей волны. Из (11.15) получаются значения координат пучностей:

х_пучн=±n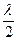 (n=0, 1, 2, …) (11.16)

Следует иметь в виду, что пучность представляет собой не одну единственную точку, а плоскость, точки которой имеют значение координаты х, определяемое формулой (11.36).

В точках, координаты которых удовлетворяют условию

2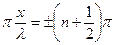 (n=0, 1, 2, …),

амплитуда колебаний обращается в нуль. Эти точки называются узлами стоячей волны. Точки среды, находящиеся в узлах, колебаний не совершают. Координаты узлов имеют значения

х_узл=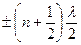 (n=0, 1, 2, …). (11.17)

Узел, как и пучность, представляет собой не одну точку, а плоскость, точки которой имеют значения координаты х, определяемые формулой (11.17).

Из формул (11.16) и (11.17) следует, что расстояние между соседними пучностями, так же как и расстояния между соседними узлами, равно l/2. Пучности и узлы сдвинуты друг относительно друга на четверть длины волны.

Обратимся снова к уравнению (11.14), множитель 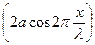при переходе через нулевое значение меняет знак. В соответствии с этим фаза колебаний по разные стороны от узла отличается на p. Это означает, что точки, лежащие по разные стороны от узла, колеблются в противофазе. Все точки, заключенные между двумя соседними узлами, колеблются синфазно (т.е. в одинаковой фазе

Дата добавления: 2013-12-11