Метод прямоугольников

Цель: вспомнить аналитический метод и познакомиться с численным методом интегрирования и практическим применением приближённого вычисления определённых интегралов

Лекция к занятию №22 по теме: Численное интегрирование

План:

1. Постановка задачи.

2. Численные методы интегрирования.

3. Метод прямоугольников.

4. Метод средних прямоугольников.

5. Пример решения задачи.

6. Контрольные вопросы.

7. Список рекомендуемой литературы.

Многие инженерные задачи, задачи физики, геометрии и многих других областей человеческой деятельности приводят к необходимости вычислять определенный интеграл вида

, (1),

где f(x) — подынтегральная функция, непрерывная на отрезке [а; b].

Пусть задана подынтегральная функция f (х), необходимо найти определенный интеграл, который вычисляется по форму­ле Ньютона — Лейбница

= F(b)-F(a). (2)

Если же интеграл от данной функции не может быть вычислен по формуле (2), или если функция f (х) задана графически или таблицей, то для вычисления определенного интеграла применяют приближенные формулы. Для приближенного вычисления инте­грала (2) существует много численных методов, таких как:

• метод прямоугольников;

• трапеций;

• Симпсона и др.

При вычислении интеграла следует помнить, каков геомет­рический смысл определенного интеграла.

*

Если f(x) ≥ 0 на отрезке [а; b], то численно равен площади фигуры, ограниченной графиком функции y=f(x), от­резком оси абсцисс, прямой х= а и прямой х= b(рис. 1). Та­ким образом, вычисление интеграла равносильно вычислению площади криволинейной трапеции.

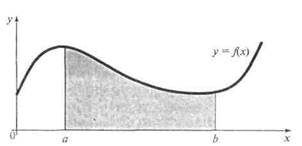
Рис. 1. Геометрический смысл интеграла

Разделим отрезок [а; b]на п равных частей, т. е. на п эле­ментарных отрезков. Длина каждого элементарного отрезка .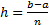

Точками деления будут: х₀ = а; х₁ = а + h; х₂ = a + 2h,...,; х_n-1 = a + (n-1)h; х_n = b. Эти числа будем называть узлами. Вы­числим значения функции f(x) в узлах, обозначим их у₀, у₁, у₂,..., у_n. Стало быть, y₀=f(a), у₁ = f (x₁), у₂=f (x₂),..., y_n=f(b). Числа у₀, у₁, у₂,..., у_n являются ординатами точек графи­ка функции, соответствующих абсциссам х₀, х₁, х₂,..., х_n (рис. 2).

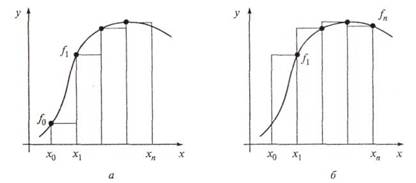
Рис. 2. Методы левых (а) и правых (б) прямоугольников

Из рис. 2. видно, что площадь криволинейной трапеции приближенно заменяется площадью многоугольника, составлен­ного из п прямоугольников. Таким образом, вычисление опреде­ленного интеграла сводится к нахождению суммы n элементар­ных прямоугольников

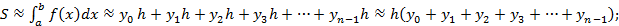(3)

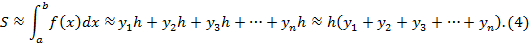
Формула (3) называется формулой левых прямоугольни­ков, (4) — правых прямоугольников, (5) — формулой сред­них прямоугольников (рис. 3).

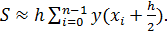(5)

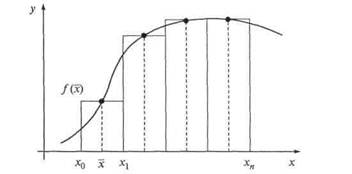
Рис. 3. Метод средних прямоугольников

Алгоритм вычисления интеграла по формуле левых прямо­угольников показан на рис. 4.

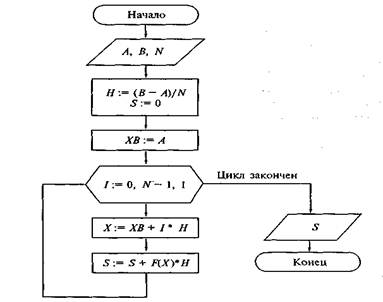
Рис. 4. Схема алгоритма вычисления интеграла

Пример С помощью метода левых и правых прямо­угольников вычислить определенный интеграл

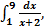полагая n=4.

Дата добавления: 2013-12-13