Плотность распределения

Непрерывные случайные величины

Определение. Случайная величина, значения которой заполняют некоторый промежуток, называется непрерывной.

Для непрерывных случайных величин выписать закон распределения невозможно. Выберем другой подход к анализу таких случайных величин, основанный на свойстве непрерывности.

Пусть x – непрерывная случайная величина. Рассмотрим для некоторого числа х вероятность попадания значения случайной величины в интервал от х до (х +D х) P (х < x < х + D х).

Ясно, что при D х ® 0 P (х < x < х + D х)® 0.

Определение. Плотностью распределения случайной величины р (х) называется предел отношения P (х < x < х + D х) к D х при D х ® 0, если такой предел существует:

.

Очевидно, что p (x) – неотрицательная функция. Для определения вероятности того, что случайная величина x примет значение из промежутка [ a, b ] конечной длины, нужно выбрать на промежутке произвольные числа x ₁, х ₂,¼, х_n, удовлетворяющие условию а=х ₀< х ₁< x ₂<¼< x_n < b=x_{n+ 1}. Эти числа разобьют промежуток [ a, b ] на (n +1) частей, представляющих собой промежутки [ х ₀, х ₁), [ х ₁, х ₂), ¼,[ х_n, b ]. Введём обозначения:

D х ₀= х ₁ – х ₀, D х ₁= х ₂ – х ₁, ¼, D х_n = b – х_n,

и составим сумму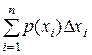. Рассмотрим процесс, при котором число точек разбиения неограниченно возрастает таким образом, что максимальная величина D х_i стремится к нулю. Будем считать функцию p (x) непрерывной на промежутке (а; b), тогда пределом суммы 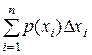будет определённый интеграл по промежутку [ a; b ] от функции p (x), равный искомой вероятности:

P (a £ x £ b) = 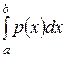. (3)

Это равенство также можно рассматривать как определение функции р (х). Отсюда следует, что вероятность попадания случайной величины в любой интервал (х ₁, х ₂) равна площади фигуры, образованной отрезком [ х ₁, х ₂] оси х,графиком функции р (х) и вертикальными прямыми х = х ₁, х = х ₂, как изображено на рисунке.

Если все возможные значения случайной величины принадлежат интервалу (а; b), то для р (х) – её плотности распределения справедливо равенство

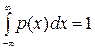
Дата добавления: 2013-12-13