Лекция к занятию №23. Формулы Ньютона-Котеса: методы прямоугольников, трапеций, метод парабол

XIX

XVIII

XVII

XVI

XV

Древнерусское государство

Аварский каганат

Гунны

Вестготы

Остготы

Черняховская культура

(Поднепровье, Поднестровье)

запад

Пиренейский п-ов

Гермонарика (германское королевство III в н.э.)

Хазарский каганат – Прикаспий. В 965 г. Разгромлен Святославом.

Днепровский союз племен во главе с полянами

+

Словено-новгородский союз племен (р. Волхов, оз. Ильмень)

=

(от Ладоги до Онеги и от Чудского озера до Волги)

кроме того: Саркел (Белая Вежа) и Тмутараканское княжество

крымчаки=половцы=сарацины

Ярослав (Юрий) à г. Юрьев à Тарту

Вятичи, кривичи – Терский берег (южное побережье Кольского п-ва)

Вторжение шведов и крестоносцев

1222 – татаро-монголы оказываются на территории половцев

В их армии десятеричная система. 10.000 = тьма. Войско состояло из покоренных народов.

Татарские ханства: Крымское, Астраханское, Казанское, Ногайская орда

Ужгород находился в составе Венгерского королевства

Тевтонцы и меченосцы объединились в Ливонский орден

На территории Финляндии: карелы, саамы, шведы

1385 – уния литовцев с Польшей; христианизация Литвы (католичество)

1380 – начало осознания себя русскими (Куликовская битва)

XV – XVI - захват берегов Финского залива шведами

Соперничество Москвы и Твери

Объединение Москвы, Твери и Новгорода. Присоединение Пскова и Рязани.

Присоединены чуваши, мордва, марийцы, башкиры, Воронеж, Елец.

Ингерманландия принимает православие и лютеранство (от шведов).

Финноязычный и славянский компоненты.

После Северной войны присоединяются карелы, ижорцы, водь, вепсы – Карелия, Прибалтика.

Также много немцев – Остзейское дворянство.

Разделы Польши 1772, 1773, 1795.

Присоединяются крымские татары.

Присоединение Финляндии.

Дальше перечень стран, не знаю к чему он:

Латвия, Эстония, Литва

Белоруссия, Украина, Бессарабия (Румыния)

Грузия, Армения, Азербайджан, Абхазия

Цель: познакомиться с формулами численного вычисления определённого интеграла.

План:

1. Предварительные соображения.

2. Формулы прямоугольников.

3. Пример решения задачи с помощью формулы прямоугольников.

4. Формулы трапеций.

5. Пример решения задачи с помощью формулы трапеций.

6. Формулы Симпсона.

7. Пример решения задачи с помощью формулы Симпсона.

8. Контрольные вопросы.

9. Список рекомендуемой литературы.

1. Предварительные соображения.

Из курса математического анализа известно, что существуют неопределённые интегралы, не выражающиеся в элементарных функциях – так называемые неберущиеся интегралы. Таким, например, является интеграл . Поэтому, очевидно, в некоторых случаях невозможно вычисление определённого интеграла с помощью формулы Ньютона-Лейбница , так как нельзя найти первообразную подынтегральной функции 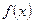. В то же время существование такого интеграла обусловлено непрерывностью функции 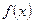на отрезке . В таких случаях прибегают к численным методам интегрирования.

Разумеется, вычислить определённый интеграл можно, непосредственно пользуясь его определением, как предел интегральных сумм: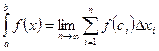, где - число отрезков разбиения (частичных отрезков), 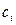- некоторые точки, произвольно выбранные на каждом из отрезков, - длина одного частичного отрезка. Однако такой способ, во-первых, достаточно громоздок, во вторых, обычно даёт результаты приемлемой точности только при больших значениях .

Чаще всего формулы приближённого вычисления определённого интеграла вытекают из его геометрического смысла. Следовательно, задача о приближённом вычислении определённого интеграла заменяется другой, равносильной ей – задачей о вычислении площади криволинейной трапеции. При этом кривая 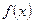заменяется другой линией, достаточно близкой к ней. В качестве этой новой линии выбирается такая кривая, для которой площадь криволинейной трапеции подсчитывается просто, то есть для которой можно легко найти первообразную. В зависимости от выбора этой кривой и различаются формулы численного интегрирования.

Предположим сначала для определённости, что 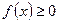для всех . Разобьём отрезок на равных частей точками 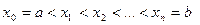. Длина каждого отрезка равна 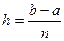. Через точки деления проведём вертикальные прямые, которые пересекут линию 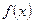в точках .

2. Формулы прямоугольников.

Заменим кривую ломаной, расположенной выше её (рисунок). Тогда определённый интеграл будет приблизительно равен площади ступенчатой фигуры, состоящей из прямоугольников:

.

Здесь 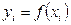- значения подынтегральной функции в правых концах отрезков разбиения.

Если же кривую заменить ломаной, расположенной ниже её, то получится формула:

.

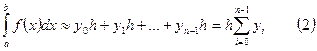Здесь 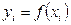- значения подынтегральной функции в левых концах отрезков разбиения. Формулы (1) и (2) называют формулами прямоугольников.

Оценка погрешности данного метода приближённого вычисления определённого интеграла находится по формуле:

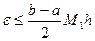(3),

где 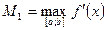- наибольшее значение первой производной подынтегральной функции на отрезке интегрирования.

Пример 1. Вычислить по одной (на выбор) из формул прямоугольников интеграл , разбив отрезок интегрирования на 10 частей. Оценить ошибку вычислений и сравнить полученное значение с точным значением, вычисленным с помощью микрокалькулятора (1,718281).

Решение.

Вычислим значения подынтегральной функции в точках деления и соответствующие значения занесём в таблицу:

х	0,0	0,1	0,2	0,3	0,4	0,5	0,6	0,7	0,8	0,9	1,0
у	1,0	1,10517	1,2214	1,34986	1,49282	1,64872	1,82212	2,01375	2,22554	2,45960	2,71828

Воспользуемся формулой (1):

.

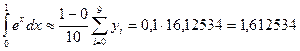Оценим ошибку вычисления. Имеем: . Подставляя в формулу (3), получаем 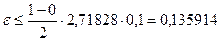. Действительно, сравнивая полученное значение с точным значением, получаем . Это весьма значительная ошибка.

Замечание. Во многих случаях формулы (1) и (2) дают приближённые значения определённого интеграла одна – с избытком, а вторая – с недостатком. Поэтому более точное значение можно получить, найдя среднее арифметическое результатов применения обеих формул.

3. Формула трапеций.

Соединив отрезками каждые две соседние точки , полученные способом, указанном в конце предыдущего пункта, заменим кривую ломаной 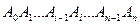. Она сверху ограничивает фигуру, составленную из прямоугольных трапеций, каждая из которых опирается на один из частичных отрезков разбиения. Площадь элементарной криволинейной трапеции с основанием заменим площадью прямоугольной трапеции, ограниченной сверху отрезком 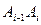. Тогда искомая площадь криволинейной трапеции, ограниченной линией , будет приближённо равна сумме площадей данных прямоугольных трапеций. Площадь каждой такой трапеции легко подсчитать, используя хорошо известную из школьного курса геометрии формулу: 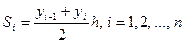. Сумма таких площадей равна:

.

После очевидных преобразований получим: 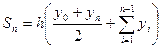. Таким образом, имеем следующую приближённую формулу вычисления определённого интеграла:

.

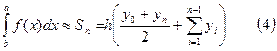Формула (4) носит название формулы трапеций. Ошибку для метода трапеций можно оценить по формуле:

,

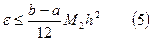где - наибольшее значение второй производной подынтегральной функции на отрезке интегрирования.

Пример 2. В условиях примера 1 использовать формулу трапеций. Оценить ошибку вычисления; сравнить полученное приближённое значение с точным.

Решение.

Воспользуемся таблицей значений, которую мы применяли в предыдущем примере.

х	0,0	0,1	0,2	0,3	0,4	0,5	0,6	0,7	0,8	0,9	1,0
у	1,0	1,10517	1,2214	1,34986	1,49282	1,64872	1,82212	2,01375	2,22554	2,45960	2,71828

Сразу по формуле (4) получаем:

.

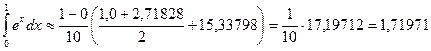Оценим ошибку вычисления. Имеем . Подставляя в формулу (5), получаем: 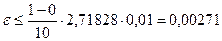. Действительно, сравнивая полученное значение с точным, получаем .

Заметим, что данный способ дал нам гораздо более точное приближение, чем используемый в предыдущем примере.

4. Формула Симпсона.

Для случаев, когда количество точек разбиения чётно, то есть , удобно использовать так называемую формулу Симпсона (параболических трапеций).

Примем её без вывода:

.

Напомним, что здесь .

Оценка ошибки при вычислении определённого интеграла методом Симпсона:

,

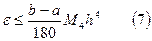где - наибольшее значение производной четвёртого порядка подынтегральной функции на отрезке интегрирования.

Пример 3. В условиях примеров 1 и 2 найти приближённое значение методом Симпсона. Оценить ошибку; сравнить полученное значение с точным.

Решение.

Воспользуемся таблицей значений, которую мы применяли в предыдущих примерах.

х	0,0	0,1	0,2	0,3	0,4	0,5	0,6	0,7	0,8	0,9	1,0
у	1,0	1,10517	1,2214	1,34986	1,49282	1,64872	1,82212	2,01375	2,22554	2,45960	2,71828

Подставим соответствующие значения в формулу (7):

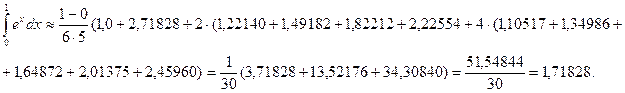(здесь )

При расчёте по данной формуле получили все 5 верных цифр после запятой. Таким образом, в одинаковых начальных условиях метод Симпсона даёт наибольшую точность приближённых вычислений определённого интеграла.

Задание.

Найти приближённые значения следующих определённых интегралов. Оценить ошибку вычисления и сравнить с точным значением. Вычисления вести с пятью знаками после запятой.

1) использовать метод прямоугольников; применить обе формулы (1) и (2), найти среднее арифметическое полученных результатов.

2) - методом трапеций.

3) 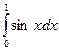- методом Симпсона.

4) - методом трапеций и методом Симпсона.

Контрольные вопросы:

1. Чем объясняется название формулы трапеций?

2. В чём выражаются преимущества формулы Симпсона перед формулой трапеций?

3. Каким образом при использовании формулы Симпсона можно рассчитывать требуемое число отрезков разбиения для достижения заданной точности ε?

Список рекомендуемой литературы:

Исаков В.Н. Элементы численных методов, стр 108-121

Поршнев С.В., Беленкова И.В. Численные методы на базе Mathcad, стр 94-100, 305-308

Дата добавления: 2013-12-13