Наїзд на нерухому перешкоду

Теорії удару в експертізе ДТП

Безпосереднє застосування теорії удару в експертізе ДТП утруднюється рядом обставин. У теорії розглядається зіткнення тел простої форми (шарообразних, плоских) і однорідних (ізотропних), пружні та міцнісні властивості яких в кожній точці тіла однакові. Автомобілі ж являють собою складні механічні системи з різними зовнішніми обриси -нями і різної внутрішньою структурою. Механічні властивості такої системи в окремих її містах можуть бути різко різними. Так, жорсткість і міцність облицювання радіатора або переднього крила незначні, а жорсткість і міцність рами або балки переднього моста досить великі. При цьому в процесі зіткнення автомобілів вони контактують не в одній точці, як це розглядається в теорії удару, а на великих ділянках зі складною конфігурацією. В ідеальному випадку вважають, що поверхні соударяющихся тел гладкі, а тертя і механічне зачеплення відсутні. Тому сили взаемодії соударяющихся тел спрямовані по нормалі до дотичної, проведеної через точку початкового контакту обох тіл. Насправді контактувати можуть одночасно кілька деталей, і на автомобіль діють кілька сил, різних за значенням, на-правлінню, тривалості і точкам додатки. У підсумку дійсні наслідки зіткнення, зокрема, швидкості і переміщення автомобілів, обчислені на підставі теорії удару, можуть не збігатися з параметрами конкретного ДТП.

Наїзд автомобіля на нерухоме абсолютно жорстке перешкоду може супроводжуватися центральним або позацентровий ударом. При центральному ударі нормаль NN до поверхонь перешкоди і автомобіля в точці їх первісного контакту проходить через центр ваги С автомобіля (мал. 24.2).

Якщо маса і жорсткість нерухомої перешкоди досить великі, а руйнування його внаслідок наїзду незначно (стіна будинку, опора моста, щогла лінії високовольтної електропередачі), то можна вважати v2=V’2 = 0. Тоді з формули (24.1) v1=- v’1 /K уд- Знак «мінус» вказує на зміну напряму швидкості при відскоку тіла від перешкоди.

До наїзду на перешкоду автомобіль може рухатися рівномірно або уповільнено. Якщо поява перешкоди в поле зору водія було несподіваним внаслідок поганої видимості або якщо водій не міг (не зумів) своєчасно загальмувати, то швидкість автомобіля остається приблизно незмінною до моменту наїзду. Можливі також випадки, коли водій встигає відреагувати на появу перешкоди і натиснути на гальмівну педаль. Однак через високу швидкість автомобіля, невеликої відстані видимості або недостатньої ефективності гальмівної системи швидкість не вдається погасити до нуля і автомобіль ударяється об перешкоду в загальмованому стані.

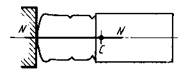
Рис. 24.2. Центральный удар

Якщо швидкість автомобіля до удару була порівняно невелика і пошкодження його внаслідок наїзду незначні, то після наїзду автомобіль відкочується від перешкоди вільно. Якщо швидкість була порівняно великою, то при ударі можливе зміщення двигуна і коробки передачі назад. Це викликає заклинювання карданної передачі, внаслідок чого блокуються задні колеса. До переднім колесам після наїзду на перешкоду зазвичай притиснуті зім'яті крила, бризковики, бампер та інші деталі, тому передні колеса також втрачають можливість обертатися. В результаті автомобіль, двигавшійся до наїзду з великою швидкістю, переміщається назад, як правило, з блокованими колесами. Якщо в період, що передував удару, водій встиг примі ¬ нитка екстрене гальмування, то після удару автомобіль може рухатися тільки «юзом», так як за вельми коротдещо час гальмівна система не може розблокувати колеса, навіть якщо нога водія зісковзне з педалі.

На мал. 24.3 показано зміну параметрів руху автомобіля при наїзді його на нерухоме тверде перешкоду у відповідності з теорією удару. Перед наездом автомобіль рухається з постійною швидкістю V1. У момент контакту з перешкодою швидкість автомобіля миттєво падає від v1 до v '1 y змінюючи знак на зворотний. Зі швидкістю v1 автомобіль відкочується від перешкоди і зупиняється під дією сил опору. Таким чином, до двох фаз удару, розглянутим вище, додається третя фаза - відкочування або «відскок» від перешкоди.

Графік на мал. 24.3, побудований у відповідності з наведеними вище визначеннями удару, має мало обного з дійсним характером процесу. За допомогою сучасної апаратури, з великою точністю фіксующей бистропротекающие явища, встановлено, що процес удару автомобілів вельми складний. Різні детали автомобіля мають при ударі різні швидкості і переміщення і навіть його центр ваги змінює своє положення внаслідок деформації деталей і зміщення вузлів і агрегатів. Тому при випробуваннях автомобіля визначають переміщення і швидкість деталі, що не деформірующейся в процесі удару (наприклад, заднього крила або заднього бампера), характеризуючи тим самим движеням автомобіля в цілому.

Мал. 24.3. Изменение скорости ав­томобиля при наезде на непо­движное препятствие

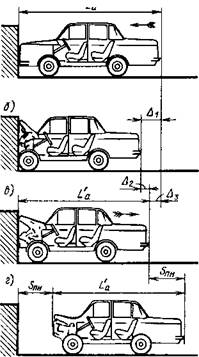
Мал. 24.4. Схема наезда автомобиля на препятствие

Процес наїзду на нерухому перешкоду ілюструє мал. 24.4. У початковий момент контакту з перешкодою (мал. 24.4, а) загальна довжина автомобіля Lа. В результаті зминання передній частині автомобіль зближується з перешкодою, рухаючись уповільнено. У момент зупинки деформація досягає максимуму і. становить ∆1 (мал. 24.4, б). Потім деталі, стислі при ударі, частково розпрямляються під дією сил пружності, і автомобіль починає рухатися прискорено в зворотному напрямку. У момент відділення від перешкоди довжина автомобіля (рис. 24.4, в). Після відділення від перешкоди автомобіль, рухаючись уповільнено, відкочується на відстань Snu (мал. 24.4, г).

Різниця розмірів La - L'a характеризує залишкову деформацію ∆з, а різниця ∆1 - ∆з являє собою пружну деформацію ∆2.

Коефіцієнтом пружності автомобіля називають відношення максимальної деформації і залишкової: Купр =∆1 / ∆з-

Розглянемо рух автомобіля в різних фазах наїзду на прикладі спрощеної моделі (мал. 24.5). Автомобіль представимо у вигляді недеформіруемое тіла з масою т. Сукупність усіх сил, прикладених до автомобіля в процесі взаємодії з перешкодою, замінимо трьома рівнодійними:

силою Рпр, прямо пропорційною переміщенню, зображуваної у вигляді умовної пружини з постійним коефіцієнтом жорсткості;

силою Рвт, прямо пропорційною швидкості переміщення (силою в'язкого тертя), представленої у вигляді рідинного амортизатора;

постійною силою (наприклад, силою сухого тертя) Рст.

Параметри, що відносяться до першої фази удару - зближенню автомобіля з перешкодою, позначимо індексом 1. тоді

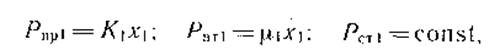
де К 1 - ПОСТІЙНИЙ коефіцієнт жорсткості пружини; м1 - постійний коефіцієнт в'язкого тертя; х1 - переміщення недеформіруемой точки тіла, наприклад, центру ваги автомобіля; х1 - швидкість тієї ж точки.

Зміна положення центра ваги автомобіля, викликане відносним переміщенням окремих деталей при ударі, їх сплющенням і зменшенням поздовжнього габариту автомобіля, не враховуємо.

Диференціальне рівняння руху такої системи:

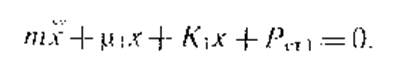(24.3)

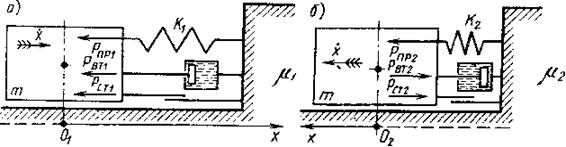
Рис. 24.5. Модель наїзду автомобіля на нерухому перешкоду: і рух в першій фазі наїзду; б - рух у другій фазі

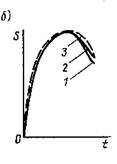
Рис. 24.6. Експериментальний графік «час - переміщення» при наїзді автомобіля на нерухому перешкоду

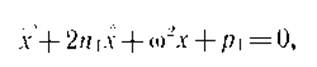(24.4)

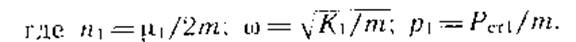
Лінійне диференціальне рівняння другого по-рядка має рішення:

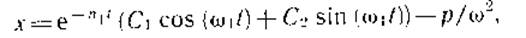(24.5)

де С1 і С2 - постійні інтегрування, які визначаються з початкових умов. Швидкість автомобіля в 'першій фазі знаходимо, про-диференціювавши формулу (24.5) за часом:

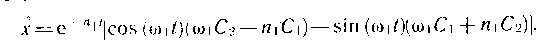(24.6)

Користуючись виразами (24.5) і (24.6), можна наити переміщення і швидкість автомобіля в будь-який момент часу t, якщо відомі початкові умови руху та характеристики системи.

Можна також вирішити і зворотну задачу: визначити невідомі характеристики по відомим параметрам руху автомобіля при наїзді його на нерухому перешкоду.

Під час полігонних випробувань на удар автомобіль наїжджає із заданою початковою швидкістю на жорстке нерухому перешкоду.

Процес удару фіксують за допомогою швидкісної кінозйомки, а також чутливих датчиків, встановлених в різних місцях автомобіля. Розшифрувавши кінограм, будують графік (рис. 24.6, а).

Початковий момент часу (t= 0) збігається з початком контакту автомобіля з перешкодою. Тангенс кута нахилу дотичної до кривої на її початковій ділянці характеризує швидкість va автомобіля перед ударом. Точка А перегину кривої означає кінець першої фази - зупинку автомобіля. Координати цієї точки відповідають часу ті руху автомобіля від початку контакту з перешкодою до зупинки і максимальну деформацію передньої частини ∆t.

Для визначення п'яти невідомих, що входять до рівняння (24.5) і (24.6), тобто С1, С2, К1, м1 i, Рст1, напишемо додаткові співвідношення. У початковий момент контакту з перешкодою, тобто при t = 0

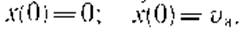(24.7)

В момент остановки автомобиля, т. е. при t= rі,

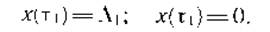(24.8)

П'яте відсутню умова знайдемо, вибравши на експериментальних графіку якусь точку і визначивши її координати. Наприклад, в момент часу ті / 2 переміщення одно х (ті / 2) =6 (точка D). Підстановка зазначених значень х і х у формули (24.5) і (24.6) дає систему з п'яти трансцендентних рівнянь, які можуть бути вирішені за допомогою ЕЦВМ. Більш просте рішення можна отримати, наскільки спростивши розрахункову схему, наприклад, припустивши, що сила сухого тертя відсутній (Рст1 = 0). Тоді, використовуючи формулу (24.7), знаходимо постійні інтегрування: Сі = 0 і C2 = va / ὠi. Після цього, застосувавши формули (24.8), отримуємо:

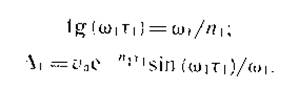(24.9 і 24.10)

Визначивши з формули (7.9) значення ri \, підставимо його у формулу (7.10). Позначивши для стислості <oiTi = A, i, прийдемо до рівняння:

(24.11)

Це рівняння містить лише одне невідоме - Інші параметри знаходять за експериментальним графіком «час - переміщення» (див. мал. 24.6). Вирішуючи рівність (24.11), знаходимо h1, а потім і інші характеристики системи.

Під час другої фази наїзду (див. рис. 24.5, б) деталі передньої частини, стислі в першій фазі, розпрямляються і автомобіль віддаляється від перешкоди. Сила Pnp становится рушійною, а сили Рвт і Рст змінюють знак на зворотний. Для позначення характеристик системи (К, м) збережемо ті ж літерні позначення, але, з огляду на зміну фізичних властивостей деталі в результаті удару, замінимо індекс 1 на 2. Початок координат 02 вибираємо в положенні, де знаходиться центр ваги в момент початку руху автомобіля у зворотному напрямку. Положительний напрям осі х - у бік руху автомобіля.

На графіку «час - переміщення» (див. мал. 24.6) друга фаза представлена ​​ділянкою кривої АВ.

Точка В відповідає моменту відриву автомобіля від перешкоди, а дотична до кривої в цій точці характеризує миттєву швидкість автомобіля va в кінці другої фази наїзду. Різниця абсцис цих точок (А і В) дає час r2 другої фази, а різницю ординат пружну деформацію ∆2. Ордината точки В (різниця ∆j -∆з) характеризує залишкову деформацію ∆з передньої частини автомобіля. Склавши рівняння руху системи і вирішивши його, можна отримати формули для визначення переміщення і швидкості автомобіля в другій фазі при відомих значеннях м2, К2, Рст2 - Так, наприклад, при Рст2 -0:

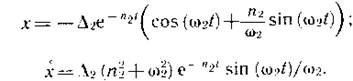(24.12)

Можна також, використавши дані експерименту, знайти коефіцієнти К2 і м2, а також силу Рст2 для фази відкату.

Для вітчизняних легкових автомобілів в першій фазі удару сила Рст1 близька до нуля, і процес удару в цій фазі добре описується рівнянням (24.11). У другій фазі сила Рст2 негативна. Це може бути результатом нелінійності коефіцієнта К2, що характеризує пружність деталей, деформованих під час першого етапу удару.

На мал. 24.6, 6 крива 1 побудована за результатами експерименту, а криві 2 і 3 отримані розрахунком. Для кривої 2 прийнято Рст2 < 0, а для кривої 3 - Рст2 -0.

За допомогою таблиць можна за формулою (24.12) знайти швидкість автомобіля в момент відділення його від перешкоди, а потім, використовуючи поняття коефіцієнта удару, визначити початкову швидкість автомобіля.

Знайти початкову швидкість автомобіля можна також, якщо на місці ДТП заміряні відстань Snн між автомобілем та перешкодою після відкоту. На експериментальному графіку (див. мал. 24.5) точка С відповідає зупинці автомобіля після його відкату від перешкоди. Різниця абсцис точок С і В визначає тривалість третьої фази т3, а різниця їх ординат - переміщення Sпн автомобіля в процесі відкату. Сума r1,r2,r3 дає загальну тривалість наїзду rн. Враховуючи короткочасність процесу відкату (триваючого менше 1 с), можна приблизно вважати всі сили, що діють при цьому на автомобіль, постійними, і рух його - равнозамедленно.

Тоді переміщення автомобіля в третій фазі

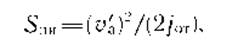
де - jот. - Уповільнення автомобіля при откативаніем від перешкоди, м/с2.

Уповільнення залежить від ступеня руйнування автомооіля при ударі. Якщо поломки порівняно невеликі і з поверхнею дороги контактують тільки шини автомобіля, то можна вважати, що уповільнення автомобіля знаходиться в межах g(jcos a + sin a) <jот< g (ὠ cosа+ sina). При цьому, як показують полігонні випробування, значення jот ближче до верхньої межі, що визначається силою зчеплення шин з дорогою. На сухому асфальтобетоні в середньому jот = 4,5-5,5 м / с.

Якщо ж швидкість автомобіля перед ударом була великою і поломки деталей великі, то можливі механическое зачеплення деформованих частин з покриттям дороги і утворення на ньому глибоких подряпин і вибоїн. У цьому випадку, як показують спостереження, уповільнення може бути значним і в деяких випадках перевищує g. Це питання вимагає подальшого вивчення.

Дата добавления: 2013-12-13