Энергия упругой волны

Плотность энергии упругой волны. Механическая энергия деформированного стержня складывается из кинетической энергии смещения элементов стержня и потенциальной энергии упругой деформации. Найдем выражение для плотности энергии стержня, испытывающего продольную деформацию удлинения или сжатия. Возьмем тонкий стержень длины 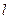. Закрепим один конец стержня, а к другому его концу приложим растягивающую (или сжимающую) силу 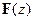, которую будем медленно увеличивать от нуля до значения 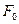. Удлинение (сжатие) стержня будет при этом изменяться от нуля до значения 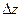. Cогласно закону Гука, 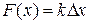, где 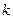– коэффициент упругости стержня. Работа силы 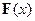в рассматриваемом процессе

Эта работа идет на увеличение потенциальной энергии стержня:

С другой стороны тот же закон Гука для относительной деформации дает

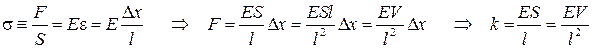
Подставляя это выражение для коэффициента упругости в формулу для потенциальной энергии, находим выражение для плотности потенциальной энергии

Пусть по тонкому стержню распространяется волна продольной деформации 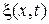со скоростью (27). Плотность упругой энергии в том месте стержня (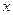), где он испытывает в данный момент () относительную деформацию 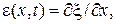равна

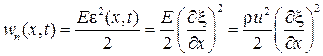
Плотность кинетической энергии в тот же момент в том же месте стержня равна.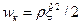

Согласно волновому уравнению, относительная деформацияи скорость смещения 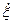при распространении продольной упругой волны пропорциональны друг другу: . Отсюда следует:

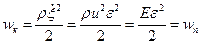
Плотность полной механической энергии тонкого стержня, по которому распространяется продольная упругая волна, равна

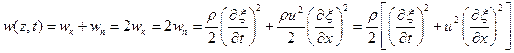
Таким образом, в упругой волне плотности кинетической и упругой энергии одинаковы и изменяются синфазно (в отличие от кинетической и потенциальной энергий колебаний). В частности, для гармонической волны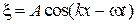

Соответствующее распределение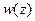вдоль стержня в некоторый момент показано на рисунке.

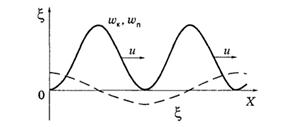
Среднее значение плотности энергии за период колебаний равно

Полученные выражения справедливы для упругих волн в жидкостях и газах.

Плотность потока энергии. При распространении волны энергия перемещается в среде вместе с возмущением. Для численного выражения процесса переноса энергии вводится понятие потока энергии Ф. Поток энергии – физическая величина, численно равная энергии, переносимой волной через определенную поверхность S в единицу времени:

Поток энергии в разных точках поверхности S может иметь разную интенсивность. Для характеристики этого обстоятельства вводят понятие плотности потока энергии. Это поток энергии через единичную площадку, перпендикулярную направлению переноса энергии:

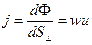
Среднее по времени значение плотности потока называют интенсивностью волны 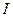= <j>.

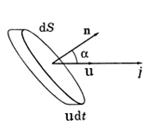Вектор Умова , 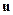- вектор скорости переноса энергии, направленный по нормали к волновой поверхности в данной точке. Зная вектор Умова в каждой точке поверхности 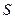, можно найти полный поток энергии через эту поверхность

Дата добавления: 2013-12-13