
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Упражнения. Таблица основных неопределенных интервалов
|
|
|
|
Таблица основных неопределенных интервалов.
1 . 8 .
8 . =
=
2 .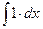 =
= =x+C 9 .
=x+C 9 .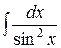 = -
= -
3. 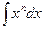 =
=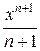 +C (n
+C (n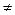 - 1 ) 10.
- 1 ) 10. 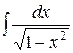 =
=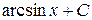
4 .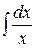 =
= 11 .
11 .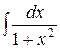 =
=  (14)
(14)
5 . =
=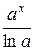 +C 12 .
+C 12 .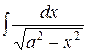 =
= 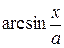 +C
+C
5* .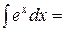 ex+C 13 .
ex+C 13 . =
=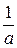
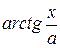 +C
+C
6.  =
=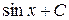 14 .
14 .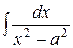 =
=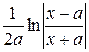 +C
+C
7 .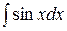 = -
= - 15 .
15 . =
=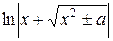 +C
+C
Используя проверку (4) для неопределенного интеграла (3), легко убедиться в истинности каждого из результатов таблицы (14). Проверим, например, первые четыре неопределенные интеграла.
1) 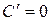 – верно;
– верно;
2)  - верно;
- верно;
3) 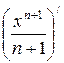 =
= - верно;
- верно;
4а) Если 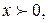 то
то 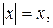 и (4) принимает вид:
и (4) принимает вид: 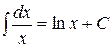 . А это верно, так как
. А это верно, так как 
4б) Если 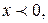 то
то  , и (4) принимает вид:
, и (4) принимает вид:  . А это верно, так как
. А это верно, так как  .
.
Совершенно аналогично дифференцированием правой части можно подтвердить и все остальные равенства в таблице (14).
Пример 5. Найти неопределенный интеграл:  .
.
Решение. Разделив числитель подынтегральной функции на знаменатель и использовав второе и третье правила интегрирования, а также таблицу основных неопределенных интегралов, получим:

Пример 5. Найти неопределенный интеграл:  .
.
Решение.

Таблица (14) содержит лишь наиболее простые неопределенные интегралы. Но в математических справочниках содержатся многие сотни (и даже тысячи) наиболее часто встречающихся на практике неопределенных интегралов. К таким справочникам относятся, например, следующие:
1.Бронштейн И.Н. и Семендяев К.А. Справочник по математике для инженеров и учащихся ВТУЗов. М., «Наука», 1981.
2.Двайт Г.Б. Таблицы интегралов и другие математические формулы. М. «Наука», 1977.
3.Градштейн И.С. и Рыжик И.М. Таблицы интегралов, сумм, рядов и произведений. М., «Наука», 1971.
Таким образом, если требуется вычислить некоторый неопределенный интеграл, то его можно просто поискать в справочнике. Если же нужного интеграла в справочнике нет, то этот интеграл, так или иначе, стараются свести к одному или нескольким табличным интегралам. О методах такого сведения мы поговорим в следующем параграфе.
А сейчас пока лишь отметим следующее важное обстоятельство, связанное с интегрированием функций (с вычислением неопределенных интегралов) и отличающее интегрирование от дифференцирования. Производная 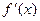 любой элементарной функции
любой элементарной функции  всегда может быть найдена, и она опять же элементарная функция. А вот неопределенный интеграл
всегда может быть найдена, и она опять же элементарная функция. А вот неопределенный интеграл 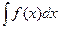 не от всякой элементарной функции
не от всякой элементарной функции  может быть записан через элементарные функции вида F(x)+C. Иначе говоря, не всякий неопределенный интеграл
может быть записан через элементарные функции вида F(x)+C. Иначе говоря, не всякий неопределенный интеграл 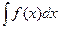 может быть сведен к табличным. А стало быть, не всякий неопределенный интеграл может быть вычислен в явном виде. Такие, не сводимые к табличным, неопределенные интегралы называются неберущимися (ибо вычислить неопределенный интеграл – это, на математическом жаргоне, «взять» интеграл). Неберущимися являются многие, даже совсем простые на первый взгляд, неопределенные интегралы. Например, такие:
может быть сведен к табличным. А стало быть, не всякий неопределенный интеграл может быть вычислен в явном виде. Такие, не сводимые к табличным, неопределенные интегралы называются неберущимися (ибо вычислить неопределенный интеграл – это, на математическом жаргоне, «взять» интеграл). Неберущимися являются многие, даже совсем простые на первый взгляд, неопределенные интегралы. Например, такие:
1.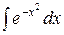 - интеграл Пуассона
- интеграл Пуассона
2. - интегральный логарифм (15)
- интегральный логарифм (15)
3.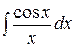 - интегральный косинус.
- интегральный косинус.
4. - интегральный синус.
- интегральный синус.
Эти и другие неберущиеся интегралы не могут быть найдены точно. Они могут быть найдены лишь приближенно. В соответствии с равенством (3) нахождение неопределенного интеграла сводится к нахождению какой-либо первообразной для подынтегральной функции. Вот эту первообразную для подынтегральной функции можно, используя компьютерные методы, подобрать приближенно с любой степенью точности.
1. Показать, что на всей числовой оси ох функция  является первообразной для функции
является первообразной для функции 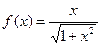 .
.
2. Найти все первообразные для функции 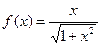
Ответ:  .
.
3. Верно ли равенство: 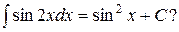
Ответ: верно.
4.Найти функцию 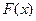 , если
, если 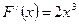 и
и  .
.
Ответ: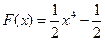 .
.
5) Используя основные свойства неопределенного интеграла и таблицу основных неопределенных интегралов, найти следующие интегралы:


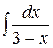


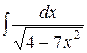

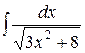

|
|
|
|
|
Дата добавления: 2013-12-13; Просмотров: 481; Нарушение авторских прав?; Мы поможем в написании вашей работы!