Интегралы от некоторых функций, содержащих квадратный трехчлен

Рассмотрим интеграл (интеграл первого типа). Преобразуем предварительно трехчлен, стоящий в знаменателе, представив его в виде суммы или разности квадратов:

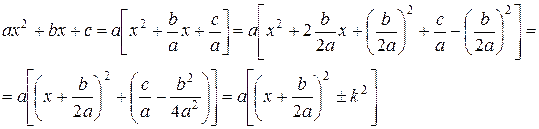
где 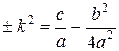. Знак плюс или минус берется в зависимости от того, будет ли выражение, стоящее слева, положительное или отрицательным, т.е. будут ли корни трехчлена 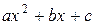комплексными или действительными.

Таким образом, исходный интеграл принимает вид:

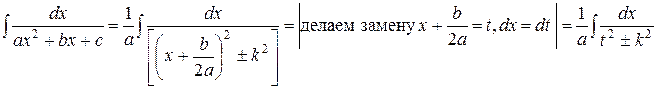т.е. мы пришли к табличным интегралам.

Пример 10. Вычислить интеграл .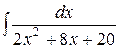

Решение:

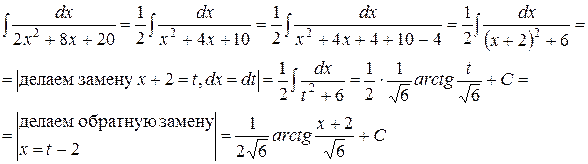
Рассмотрим интеграл более общего вида 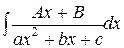(интеграл второго типа). Произведем тождественное преобразование подынтегральной функции:

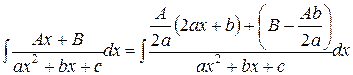
Последний интеграл представим в виде суммы двух интегралов. Вынося постоянные множители за знак интегралов, получим:

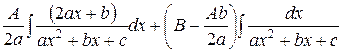
второй интеграл мы только что научились вычислять. Это интеграл первого типа. В первом интеграле сделаем замену переменного .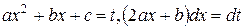

Следовательно, 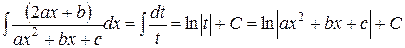. Таким образом, окончательно получаем: .

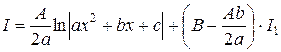Пример 11. Вычислить интеграл .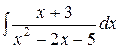

Решение:

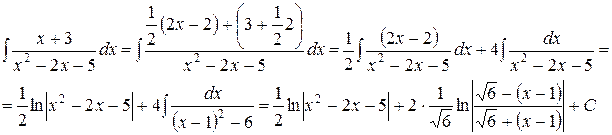
Перейдем к усложненному варианту интеграла первого типа и рассмотрим интеграл 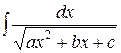(интеграл третьего типа). Выполним преобразования, аналогичные преобразованиям проведенным с интегралом первого типа. Интеграл сведется, в зависимости от знака а, к табличным интегралам вида 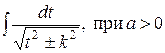или .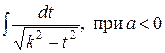

Пример 12. Вычислить интеграл .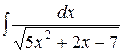

Решение: Выделив в знаменателе подынтегральной функции полный квадрат, получим

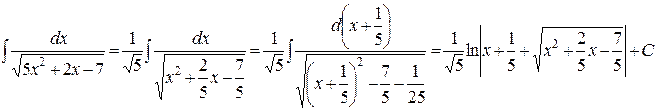
И наконец, интеграл 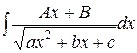(интеграл четвертого типа). Он вычисляется с помощью преобразований, аналогичных проведенных в случае интеграла второго типа.

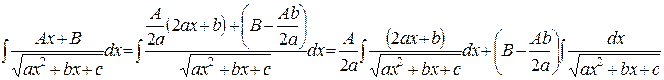
Применим к первому из полученных интегралов подстановку 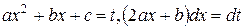, получим

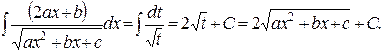
Второй же интеграл является уже рассмотренным интегралом третьего типа.

Пример 13. Вычислить интеграл .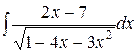

Решение: Представим данный интеграл в виде суммы двух интегралов, предварительно выделив в числителе подынтегральной функции слагаемое, равное производной подкоренного выражения из знаменателя:

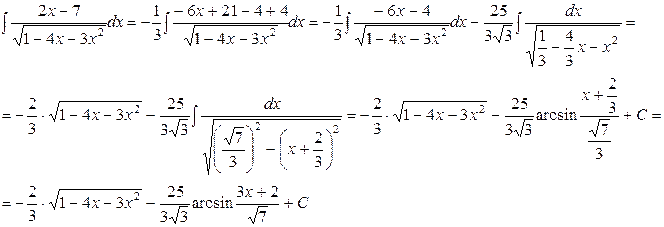
Дата добавления: 2013-12-13