Использование четности-нечетности подынтегральной функции при вычислении определенных интегралов с симметричными пределами интегрирования

Лекция 40. Вычисление определенного интеграла. Замена переменной в определенном интеграле. Интегрирование по частям. Некоторые приложения определенных интегралов. Понятие о несобственных интегралах.

Подстановка в определенных интегралах.

Пусть y = f(x) – непрерывная на промежутке [ a; b ] оси ox функция, а - непрерывная на промежутке [ α; β ] функция, имеющая к тому же на [ α;β ] непрерывную производную (то есть x=φ(t) – непрерывно дифференцируемая на [ α; β ] функция). Кроме того, будем считать, что когда переменная t меняется от α до β, то переменная x = φ(t) меняется от a до b. Таким образом, φ(α) = b и φ(β) = b. Тогда при вычислении можно совершить подстановку по следующей схеме:

 

x	a b
t	α β

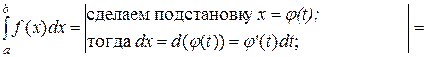
(1)

Докажем правомочность схемы (1). Пусть

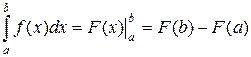
(2)

Здесь F(x) – некоторая первообразная для функции f(x). То есть F΄(x) = f(x). Но тогда, по правилу вычисления производной сложной функции,

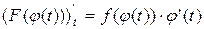
(3)

Поэтому по формуле Ньютона-Лейбница

(4)

Равенство результатов (2) и (4) и доказывает правомочность схемы (1).

Кстати, сравнивая схему (1) вычисления определенных интегралов с помощью подстановки с аналогичной схемой вычисления неопределенных интегралов, можно увидеть и то, что в этих схемах общее, и то, что различно.

Примечание. На практике часто бывает удобнее делать подстановку не вида x = φ(t), а вида t = φ(x).

Вычисление определенных интегралов по частям.

Мы уже знаем, что по частям можно вычислять неопределенные интегралы. Для этого используется уже полученная формула . Но по частям можно вычислять и определенные интегралы. Это делается по внешне похожей формуле (5):

(5)

Здесь и – любыедве непрерывные на [ a; b ] функции, имеющие на этом промежутке и непрерывные производные 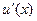и (то есть и - непрерывно дифференцируемые на [ a; b ] функции).

Докажем формулу (5). Учтем, что

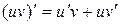
(6)

Функция , стоящая в этом равенстве справа, согласно указанных выше условий для функций и , является непрерывной на промежутке [ a; b ]. Значит, существует определенный интеграл от нее:

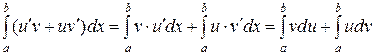
(7)

С другой стороны, согласно (6), функция является первообразной для функции . А значит, по формуле Ньютона-Лейбница получаем:

(8)

Сравнивая (7) и (8), приходим к доказываемой формуле (5).

Пример 1. Вычислить .

Решение:

а) Если f(x) – непрерывная и четная на промежутке [- a; а ] функция, то

(9)

б) Если f(x) – непрерывная и нечетная на промежутке [ -a; a ] функция, то

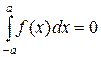
(10)

Доказательство. Рассмотрим рисунки 1(а) и 1(б), соответствующие случаям (а) и (б) соответственно.

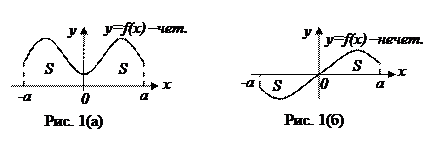
а) Если f(x) – четная на [- a; a ] функция, то согласно рис.1(а) и формулы (3) получаем:

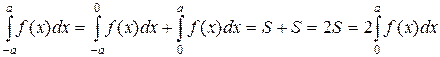
б) Если f(x) – нечетная на [ a; b ] функция, то согласно рис. 1(б) и формулам (3) и (5) получаем:

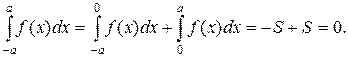
Пример 2. Упростить, а затем и вычислить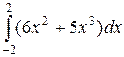

Решение.

Дата добавления: 2013-12-13