Энтропия и информация

Примеры систем и структур.

Система элементов Д.И.Менделеева 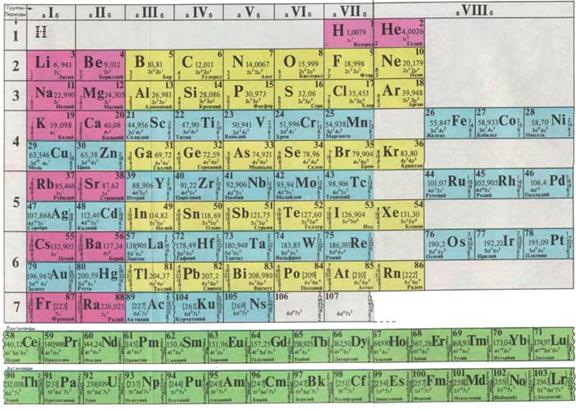Системы в биологии
7 кристаллических систем	Решетки Бравэ в кристаллографии
Cтруктура кристалла NaCl	Структура молекулы ДНК
Cтруктура кристалла алмаза	Структура графита

Понятие энтропии как меры хаоса возникло в молекулярной физике при анализе теплового движения молекулC:\temp\Естествознание КСЕ\HTML\Video\video3.htm и поэтому мы вынуждены далее рассматривать состояние и процессы в термодинамических системах.

Самым простым примером хаотического состояния движения в веществе является, как мы отмечали в первом пункте, движение молекул газа или жидкости, которое можно наблюдать с помощью «броуновских» мелких частиц, взвешенных в среде, как пылинки в воздухе. Беспорядочное движение в системе было названо тепловым и подробно изучено в термодинамике и молекулярной (статистической) физике. Исследование термодинамических систем (ТС) наиболее просто проводить в состоянии их равновесия с окружающими телами. Переход из одного равновесного состояния в другое в термодинамике названо процессом. При этом зависимость параметров от времени не учитывается. Параметры: давление (p), объем (V), температура (T) и энтропия (S) являются макропараметрами системы и характеризуют ее «в целом». Такой подход назовем системным или феноменологическим.

Раздел термодинамики, изучающий процессы, при которых параметры состояния зависят от времени, называется кинетикой.

Возможен и другой, структурный подход к термодинамическим системам, при котором учитывается внутреннее, например, молекулярное строение системы. В этом случае вводятся микропараметры, такие как координата "i"-й молекулы или длина ее свободного пробега (l _i) от одного удара до другого при взаимодействии с соседними молекулами, импульс молекулы (p_i), изменение которого при ударе создает давление в газе, энергия молекулы (ε_i) и, наконец, статистическая энтропия, как характеристика беспорядка в отдельных подсистемах (σ_i). Связь между способами описания представлена на схеме:

Способы описания термодинамических систем

Впервые понятие энтропии было введено Клаузиусом в 1865 г. как функция термодинамического состояния системы. Эта функция имеет вид

(Q – теплота, T - температура). Классики не связывали энтропию с информацией. Энтропия была получена эмпирически, в экспериментах с газами.

Анализ этой функции показал, что физический смысл энтропии проявляется, как часть внутренней энергии системы, которая не может быть превращена в работу.

Л.Больцман (1872г.) методами статистической физики вывел теоретическое выражение энтропии S = K lnW, где К – константа; W – термодинамическая вероятность (количество перестановок молекул идеального газа, не влияющее на макросостояние системы). Энтропия Больцмана выведена для идеального газа и трактуется как мера беспорядка, мера хаоса системы. Для идеального газа энтропии Больцмана и Клаузиуса тождественны, поэтому и эмпирическая функция Клаузиуса стала объясняться как мера вероятности состояния молекулярной системы. Формула Больцмана стала настолько знаменитой, что начертана в качестве эпитафии на его могиле. Сложилось мнение, что энтропия и беспорядок есть одно и тоже. Несмотря на то, что энтропия описывает лишь один класс объектов Мира (идеальные газы), ее не критично стали привлекать для описания более сложных объектов.

Сам Больцман в 1886г. попытался с помощью энтропии объяснить, что такое жизнь. По мнению Больцмана, жизнь это явление, способное уменьшать свою энтропию. «Всеобщая борьба за существование это борьба против энтропии». Согласно Больцману и его последователям, все процессы во Вселенной изменяются в направлении хаоса. Вселенная идет к тепловой смерти. Этот мрачный прогноз долго господствовал в науке. Однако углубление знаний об окружающем Мире постепенно расшатали эту догму.

Антитезой Больцману выступали эволюционисты. В частности Ч.Дарвин показал, что процессы жизни не только не деградируют, но все время усложняются. И если прав Больцман, то почему мы до сих пор еще живем.

Первая половина XX века принесла человечеству модель рождения и эволюции Вселенной, где над деструктивными процессами преобладали процессы самоорганизации материи. Вселенная всегда самоусложнялась и этот процесс, начавшийся 15-20 млрд. лет назад, продолжается до сих пор. Таким образом, считается, что в природе существуют два перехода порядок→хаос и его противоположность хаос→порядок. В изолированных системах (но не всегда) идет процесс перевода порядка в хаос. В открытых системах, через которые проходят созидательные потоки энергии, могут идти процессы самоорганизации и на фоне хаоса рождается порядок. Существует и альтернативное мнение утверждающее, что порядок рождается только из предшествующего порядка.

Пренебрегая взаимодействием между частицами и внешними воздействиями на систему, Больцман упростил Мир до предела, представив его идеальным газом, не учитывая того, что все молекулы обладают своей внутренней структурой, взаимодействуют друг с другом, находятся в поле тяжести, совершают колебательные движения и т.д.

В расширяющейся Вселенной наблюдается тенденция не к выравниванию градиентов и потенциалов, а к расслоению. Из однородного первичного гелий-водородного облака путем гравитационного сжатия стали образовываться плотные сгустки материи: звезды, планеты. Вселенная становилась неоднородной, как по плотности, так и по температуре. Химический состав ее усложнялся. Кроме простых атомов водорода и гелия возникли в недрах звезд все элементы таблицы Менделеева. Появилась жизнь. Разве это деградация?

Когда говорят о неоднородности какой – либо среды, имеют в виду то, что в каждой единице объема содержится одинаковое количество каких-либо элементов. Считается, что газ - это однородная среда, если рассматривать 1смобъема. Но если рассматривать и сравнивать микрообъемы, соизмеримые с размерами молекул, то окажется, что среда очень неоднородная. В одной такой единице объема может находиться одна молекула, а в другой - ни одной. Вселенная однородна в мегамасштабах, но в размерах галактик очень неоднородна.

Как совместить рост энтропии при понижении температуры Вселенной (S=Q/T) c нарисованной картиной усложнения. Надо думать, что в погоне за математической простотой Больцман так упростил модель своего исследования, что область применения выводов осталась справедливой только в изолированных системах (для идеальных газов).

В реальных молекулярных системах существуют два вида энергии: потенциальная (энергия связей) и кинетическая (энергия движения молекул). Больцман потенциальную энергию не учитывал. Но формула Клаузиуса, являясь эмпирической, автоматически учитывала все виды энергии. Поэтому значения энтропий Больцмана и Клаузиуса совпадают только в применении к идеальным газам, где доля потенциальной энергии невелика. Для расчетов энтропии жидкостей и твердых тел с высоким значением потенциальной энергии используют, как правило, только энтропию Клаузиуса (S=Q/T).

Во Вселенной относительно стационарные структуры существуют только благодаря силам взаимодействия, но именно эти силы энтропия Больцмана не учитывает. Поэтому прогноз тепловой смерти Вселенной ошибочен.

Приведем примеры. Звезда (солнце) возникает вследствие гравитационного сжатия газа (гравитационное взаимодействие). Если бы исчезла гравитация, то облако плазмы, в полном согласии с Больцманом, из-за внутреннего давления начало бы неограниченно расширяться, увеличивая беспорядок (энтропию).

В ходе однонаправленного течения реки в потоке могут возникать вихри (организованности). Если бы вода в реке не находилась под влиянием гравитационного поля Земли (силы тяжести), то не было бы течения и вихри (упорядоченное движение) не возникали бы при этом.

В качестве примера самоорганизации очень часто приводят эффект, обнаруженный Бенаром (1900г.). Слой масла на нагретой сковородке иногда может образовать упорядоченную структуру в виде сот (ячейки Бенара). Это результат конвекции, а она может происходить только в поле тяжести Земли. В невесомости ячейки Бенара не возникли бы. Так что игнорирование в расчетах сил взаимодействия может исказить выводы, что и произошло у Больцмана.

Несмотря на неоднократное напоминание в известных публикациях, что формула энтропии имеет ограниченное применение [305, 306], её все же пытаются с легкой руки Больцмана применить ко всей Вселенной. Например, Седов А. в своей книге «Одна формула и весь мир» пытается показать универсальность понятия энтропии. Биологи стремятся доказать, что все живое в ходе жизнедеятельности уменьшает свою энтропию и это есть признак жизни.

Понятие энтропия оказалось удобным, но не очень корректным. Им продолжают пользоваться не только биологи, но и социологи. Например, Н.Алексеев в своей статье пытается применить понятие энтропии для описания функционирования некоторой организации. Он утверждает, что «эволюция экономических систем происходит за счет роста энтропии природной среды…».

По мнению Штеренберга, в формуле Клаузиуса S=Q/T энергия есть некоторая сумма всех видов энергий системы: кинетической, потенциальной и любых других. Но беспорядочность молекулярной системы обычно связывают с кинетической энергией движения молекул. Чем выше кинетическая энергия всех видов движения молекул (предполагая, что все направления движения равновероятны), тем больше хаоса. Но возможность совершать работу зависит как от потенциальной, так и от кинетической энергии. Сложное «переплетение» разных видов энергии в реальных системах делает энтропию очень нечеткой функцией. Ее безусловная область применения это системы, из которых ее выводили – идеальный газ. Переход к жидкому и твердому состоянию уже вызывает многие отклонения.

Сопоставим теперь энтропию Шеннона с энтропией Больцмана и Клаузиуса. Очевидно, что формулы Шеннона и Клаузиуса совершенно не схожи. В последней фигурирует температура, которую к теории связи никак не применишь. Но формулы Больцмана (S=KlnW) и Шеннона (H=-∑P_i log₂P_i) имеют некоторое внешнее сходство. Рассмотрим крайние случаи. Допустим, по каналу связи передается один и тот же сигнал (буква А и пауза) и никаких помех нет. Вероятность обнаружить сигнал А равна ½.Тогда H = (1/2log₂1/2+1/2log₂1/2)=1. Это означает, что по каналу передается количество информации Y = log₂ 2 =1 бит. Смысл информации Шеннона сводится к достоверному отличию одного сигнала от другого. Например, отличию сигнала на входе канала от сигнала на выходе. Бесспорно для теории связи метод оценки достоверности сигнала, предложенный Шенноном, сыграл большую роль. Известный физик Луи де Бройль назвал энтропию Шеннона наиболее важной идеей кибернетики. Сходство S и Н в том, что стремление к равновероятности (однородности) состояний системы увеличивает обе энтропии. Но в энтропии Больцмана нет верхнего предела S. Чем больше W, тем выше S. У Шеннона H_max = 1.

Подведем итоги. Известно три варианта энтропий. В термодинамике - это функция состояния (Клаузиус) и мера беспорядка (Больцман). В теории информации – мера достоверности передаваемой по каналу связи информации (Шеннон).

Дата добавления: 2013-12-13